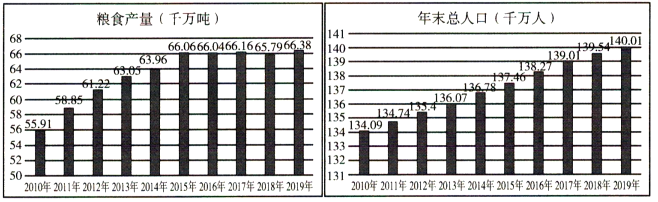
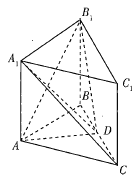
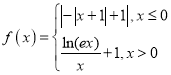题目内容
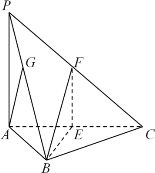
【题目】已知三棱柱
平面
是
内一点，点
在直线
上运动，若直线
和
所成角的最小值与直线
和平面
所成角的最大值相等，则满足条件的点
的轨迹是（ ）
A.直线的一部分B.圆的一部分C.抛物线的一部分D.椭圆的一部分
【答案】C
【解析】
过点
作
平面
，垂足为点
，则由最小角定理得直线
和
所成角的最小值为直线与平面所成的角
，直线
与平面所成的角为
，根据题意利用正弦函数可得点在平面内的轨迹为抛物线的一部分，可得结论.
过点作平面，垂足为点，则由最小角定理得直线和所成角的最小值为直线与平面所成的角.
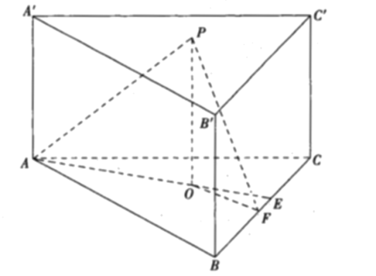
直线与平面所成的角为，
因为
为定值，所以如果最大，则
最小，当
时， 取得最小值为点到直线
的距离，
又因为
，则由直线和所成角的最小值与直线与平面所成角的最大值相等，可得点到点
的距离等于点到直线的距离，
所以点在平面内的轨迹为抛物线的一部分，则点在平面
内的轨迹为抛物线的一部分.
故选C.
练习册系列答案
天天向上一本好卷系列答案
小学生10分钟应用题系列答案
相关题目
