题目内容
【题目】已知函数![]() .
.
(Ⅰ)设![]() ,讨论
,讨论![]() 的单调性;
的单调性;
(Ⅱ)若对任意![]() 恒有
恒有![]() ,求
,求![]() 的取值范围.
的取值范围.
【答案】(1)当![]() 时,
时,![]()
所以![]() 上为增函数
上为增函数
②当![]() ,由
,由![]()
![]() 上为增函数,
上为增函数,
在![]() 上是减函数
上是减函数
(2)![]()
【解析】
试题(I)![]() 的定义域为(
的定义域为(![]() ,1)
,1)![]() (1,
(1,![]() )
)
![]()
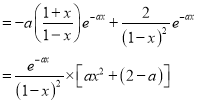
因为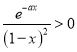 (其中
(其中![]() )恒成立,所以
)恒成立,所以![]()
⑴ 当![]() 时,
时,![]() 在(
在(![]() ,0)
,0)![]() (1,
(1,![]() )上恒成立,所以
)上恒成立,所以![]() 在(
在(![]() ,1)
,1)![]() (1,
(1,![]() )上为增函数;
)上为增函数;
⑵ 当![]() 时,
时,![]() 在(
在(![]() ,0)
,0)![]() (0,1)
(0,1)![]() (1,
(1,![]() )上恒成立,所以
)上恒成立,所以![]() 在(
在(![]() ,1)
,1)![]() (1,
(1,![]() )上为增函数;
)上为增函数;
⑶ 当![]() 时,
时,![]() 的解为:(
的解为:(![]() ,
,![]() )
)![]() (t,1)
(t,1)![]() (1,+
(1,+![]() )
)
(其中![]() )
)
所以![]() 在各区间内的增减性如下表:
在各区间内的增减性如下表:
区间 | ( | ( | (t,1) | (1,+ |
| + |
| + | + |
| 增函数 | 减函数 | 增函数 | 增函数 |
(II)显然![]()
⑴ 当![]() 时,
时,![]() 在区间
在区间![]() 0,1
0,1![]() 上是增函数,所以对任意
上是增函数,所以对任意![]() (0,1)都有
(0,1)都有![]() ;
;
⑵ 当![]() 时,
时,![]() 是
是![]() 在区间
在区间![]() 0,1
0,1![]() 上的最小值,即
上的最小值,即![]() ,这与题目要求矛盾;
,这与题目要求矛盾;
⑶ 若![]() ,
,![]() 在区间
在区间![]() 0,1
0,1![]() 上是增函数,所以对任意
上是增函数,所以对任意![]() (0,1)都有
(0,1)都有![]() 。
。
综合⑴、⑵、⑶ ,a的取值范围为(![]() ,2)
,2)

练习册系列答案
相关题目
【题目】某超市随机选取![]() 位顾客,记录了他们购买甲、乙、丙、丁四种商品的情况,整理成如下统计表,其中“√”表示购买,“×”表示未购买.
位顾客,记录了他们购买甲、乙、丙、丁四种商品的情况,整理成如下统计表,其中“√”表示购买,“×”表示未购买.
| 甲 | 乙 | 丙 | 丁 |
| √ | × | √ | √ |
| × | √ | × | √ |
| √ | √ | √ | × |
| √ | × | √ | × |
85 | √ | × | × | × |
| × | √ | × | × |
(Ⅰ)估计顾客同时购买乙和丙的概率;
(Ⅱ)估计顾客在甲、乙、丙、丁中同时购买![]() 中商品的概率;
中商品的概率;
(Ⅲ)如果顾客购买了甲,则该顾客同时购买乙、丙、丁中那种商品的可能性最大?