题目内容
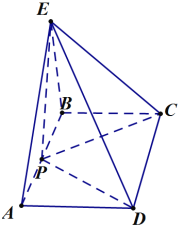
【题目】如图,在矩形ABCD中,AB=2BC,P是线段AB中点,![]() 平面ABCD.
平面ABCD.
(1)求证:![]() 平面EPC;
平面EPC;
(2)问在EP上是否存在点F,使平面![]() 平面BFC?若存在,求出
平面BFC?若存在,求出![]() 的值;若不存在请说明理由.
的值;若不存在请说明理由.
【答案】(1)详见解析;(2)存在,![]() ,理由见解析.
,理由见解析.
【解析】
(1)由已知得∠APD=∠BPC=45°,∠DPC=90°,从而DP⊥PC,由EP⊥平面ABCD,得EP⊥DP,由此能证明DP⊥平面EPC.
(2)假设存在F,使平面AFD⊥平面BFC,由已知得AD∥平面BFC,从而AD平行于平面AFD与平面BFC的交线l,由已知得EP⊥AD,而AD⊥AB,从而l⊥平面FAB,∠AFB为平面AFD与平面BFC所成二面角的平面角,由此能求出当![]() 时,平面AFD⊥平面BFC.
时,平面AFD⊥平面BFC.
解:(1)证明:∵在矩形ABCD中,AB=2BC,
P、Q分别是线段AB,CD中点,
∴∠APD=∠BPC=45°,∴∠DPC=90°,∴DP⊥PC,
∵EP⊥平面ABCD,DP平面ABCD,
∴EP⊥DP,
又PC∩EP=P,∴DP⊥平面EPC.
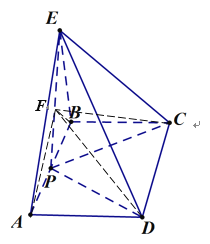
(2)解:假设存在F,使平面AFD⊥平面BFC,
∵AD∥BC,BC平面BFC,AD不包含于平面BFC,
∴AD∥平面BFC,
∴AD平行于平面AFD与平面BFC的交线l,
∵EP⊥平面ABCD,
∴EP⊥AD,而AD⊥AB,
AB∩EP=P,∴AD⊥平面EAB,∴l⊥平面FAB,
∴∠AFB为平面AFD与平面BFC所成二面角的平面角,
∵P是AB的中点,且FP⊥AB,
∴当∠AFB=90°时,FP=AP,
∴当![]() 时,平面AFD⊥平面BFC.
时,平面AFD⊥平面BFC.

 互动课堂系列答案
互动课堂系列答案 激活思维智能训练课时导学练系列答案
激活思维智能训练课时导学练系列答案【题目】世界那么大,我想去看看,每年高考结束后,处于休养状态的高中毕业生旅游动机强烈,旅游可支配收入日益增多,可见高中毕业生旅游是一个巨大的市场.为了解高中毕业生每年旅游消费支出(单位:百元)的情况,相关部门随机抽取了某市的1000名毕业生进行问卷调查,并把所得数据列成如下所示的频数分布表:
组别 |
|
|
|
|
|
频数 |
|
|
|
|
|
(1)求所得样本的中位数(精确到百元);
(2)根据样本数据,可近似地认为学生的旅游费用支出![]() 服从正态分布
服从正态分布![]() ,若该市共有高中毕业生35000人,试估计有多少位同学旅游费用支出在 8100元以上;
,若该市共有高中毕业生35000人,试估计有多少位同学旅游费用支出在 8100元以上;
(3)已知本数据中旅游费用支出在![]() 范围内的8名学生中有5名女生,3名男生, 现想选其中3名学生回访,记选出的男生人数为
范围内的8名学生中有5名女生,3名男生, 现想选其中3名学生回访,记选出的男生人数为![]() ,求
,求![]() 的分布列与数学期望.
的分布列与数学期望.
附:若![]() ,则
,则![]() ,
,![]() ,
,![]() .
.
【题目】某个体经营者把开始六个月试销A、B两种商品的逐月投资与所获纯利润列成下表:
投资A商品金额(万元) | 1 | 2 | 3 | 4 | 5 | 6 |
获纯利润(万元) | 0.65 | 1.39 | 1.85 | 2 | 1.84 | 1.40 |
投资B商品金额(万元) | 1 | 2 | 3 | 4 | 5 | 6 |
获纯利润(万元) | 0.25 | 0.49 | 0.76 | 1 | 1.26 | 1.51 |
该经营者准备下月投入12万元经营这两种产品,但不知投入A、B两种商品各多少才最合算.请你帮助制定一下资金投入方案,使得该经营者能获得最大利润,并按你的方案求出该经营者下月可获得的最大利润(结果保留两个有效数字).