题目内容
【题目】![]() 两个居民小区的居委会欲组织本小区的中学生,利用双休日去市郊的敬老院参加献爱心活动.两个校区每位同学的往返车费及服务老人的人数如下表:
两个居民小区的居委会欲组织本小区的中学生,利用双休日去市郊的敬老院参加献爱心活动.两个校区每位同学的往返车费及服务老人的人数如下表:
|
| |
往返车费 | 3元 | 5元 |
服务老人的人数 | 5人 | 3人 |
根据安排,去敬老院的往返总车费不能超过37元,且![]() 小区参加献爱心活动的同学比
小区参加献爱心活动的同学比![]() 小区的同学至少多1人,则接受服务的老人最多有____人.
小区的同学至少多1人,则接受服务的老人最多有____人.
【答案】![]()
【解析】分析:设![]() 两区参加活动同学的人数分别为
两区参加活动同学的人数分别为![]() ,受到服务的老人人数为
,受到服务的老人人数为![]() ,
,
找出约束条件与目标函数,准确地描画可行域,平移直线可求得满足题设的最优解.
详解:
设![]() 两区参加活动同学的人数分别为
两区参加活动同学的人数分别为![]() ,受到服务的老人人数为
,受到服务的老人人数为![]() ,
,
则![]() ,且
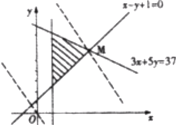
,且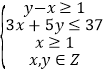 作出可行域,如图
作出可行域,如图
平移直线![]() ,由图可知,
,由图可知,
当直线![]() 过点
过点![]() 时,
时,![]() 最大,
最大,
![]() 当
当![]() 时,
时,![]() 取得最大值为
取得最大值为![]() ,
,
即接受服务的老人最多有![]() 人,故答案为
人,故答案为![]() .
.

练习册系列答案
相关题目
【题目】国家环境标准制定的空气质量指数与空气质量等级对应关系如表:
空气质量指数 | 0~50 | 51~100 | 101~150 | 151~200 | 201~300 | 300以上 |
空气质量等级 | 1级优 | 2级良 | 3级轻 度污染 | 4级中度污染 | 5级重 度污染 | 6级严重污染 |
由全国重点城市环境监测网获得10月份某五天甲城市和乙城市的空气质量指数数据用茎叶图表示如图:
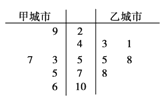
(1)试根据上面的统计数据,计算甲、乙两个城市的空气质量指数的方差;
(2)试根据上面的统计数据,估计甲城市某一天空气质量等级为2级良的概率;
(3)分别从甲城市和乙城市的统计数据中任取一个,试求两个城市空气质量等级相同的概率.供参考数据:292+532+572+752+1062=23760,432+412+552+582+782=16003
