Question

【题目】已知椭圆的离心率为，焦点分别为，点是椭圆上的点，面积的最大值是．

（Ⅰ）求椭圆的方程；

（Ⅱ）设直线与椭圆交于两点，点是椭圆上的点，是坐标原点，若判定四边形的面积是否为定值？若为定值，求出定值；如果不是，请说明理由．

Answer 1

【答案】（Ⅰ） （Ⅱ）见解析

【解析】

（Ⅰ）由题意得到的方程组，求出的值，即可得出椭圆方程；

（Ⅱ）当直线的斜率不存在时，易求出四边形的面积；当直线的斜率存在时，设直线方程是，联立直线与椭圆方程，结合判别式和韦达定理，可表示出弦长，再求出点到直线的距离，根据和点在曲线上，求出的关系式，

最后根据，即可得出结果.

解：（Ⅰ）由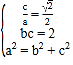解得 得椭圆的方程为.

（Ⅱ）当直线的斜率不存在时，直线的方程为或，此时四边形的面积为．

当直线的斜率存在时，设直线方程是，联立椭圆方程

，

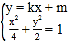
点到直线的距离是

由得

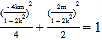因为点在曲线上，所以有整理得

由题意四边形为平行四边形，所以四边形的面积为

由得, 故四边形的面积是定值，其定值为．