题目内容
已知数列{an}满足a1=
,2an+1=3an-1.
(1)求a2,a3,a4;
(2)证明数列{an-1}是等比数列,并求{an}的通项公式.
| 5 |
| 2 |
(1)求a2,a3,a4;
(2)证明数列{an-1}是等比数列,并求{an}的通项公式.
(1)由2an+1=3an-1,得an+1=
an-
…(1分)
所以a2=
a1-
=
…(2分)
a3=
a2-
=
,…(3分)
a4=
a3-
=
…(4分)
(2)由an+1=
an-
,得an+1-1=
(an-1)…(6分)
所以数列{an-1}是首项为a1-1=
,公比为
的等比数列…(8分)
所以an-1=(
)n…(10分)
所以an=(
)n+1…(12分)
| 3 |
| 2 |
| 1 |
| 2 |
所以a2=
| 3 |
| 2 |
| 1 |
| 2 |
| 13 |
| 4 |
a3=
| 3 |
| 2 |
| 1 |
| 2 |
| 35 |
| 8 |
a4=
| 3 |
| 2 |
| 1 |
| 2 |
| 97 |
| 16 |
(2)由an+1=
| 3 |
| 2 |
| 1 |
| 2 |
| 3 |
| 2 |
所以数列{an-1}是首项为a1-1=
| 3 |
| 2 |
| 3 |
| 2 |
所以an-1=(
| 3 |
| 2 |
所以an=(
| 3 |
| 2 |

练习册系列答案
相关题目
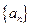 ,
,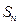 是其前
是其前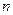 项的和,且
项的和,且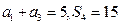 .
.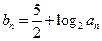 ,求数列
,求数列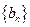 的前
的前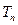 ;
;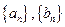 满足
满足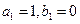 且
且
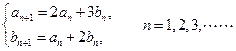
 的值,使得数列
的值,使得数列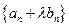 为等比数列;(Ⅱ)求数列
为等比数列;(Ⅱ)求数列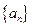 和
和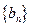 的通项公式;
的通项公式;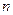 项和分别为
项和分别为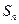 和
和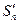 ,求极限
,求极限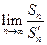 的值.
的值.