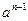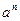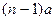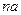题目内容
设数列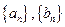 满足
满足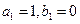 且
且
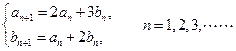
(Ⅰ)求 的值,使得数列
的值,使得数列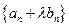 为等比数列;(Ⅱ)求数列
为等比数列;(Ⅱ)求数列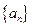 和
和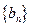 的通项公式;
的通项公式;
(Ⅲ)令数列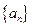 和
和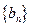 的前
的前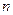 项和分别为
项和分别为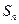 和
和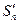 ,求极限
,求极限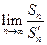 的值.
的值.
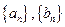 满足
满足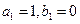 且
且
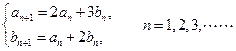
(Ⅰ)求
 的值,使得数列
的值,使得数列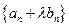 为等比数列;(Ⅱ)求数列
为等比数列;(Ⅱ)求数列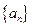 和
和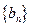 的通项公式;
的通项公式;(Ⅲ)令数列
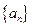 和
和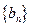 的前
的前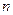 项和分别为
项和分别为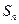 和
和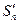 ,求极限
,求极限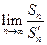 的值.
的值.(Ⅰ) (Ⅱ)
(Ⅱ)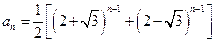 ,
,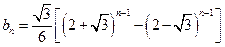 .
.
(Ⅲ)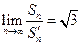
 (Ⅱ)
(Ⅱ)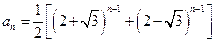 ,
,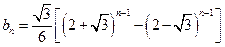 .
.(Ⅲ)
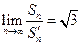
(Ⅰ)令 ,其中
,其中 为常数,若
为常数,若 为等比数列,则存在
为等比数列,则存在 使得
使得
 .
.
又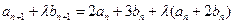
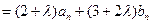 .
.
所以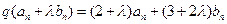 .
.
由此得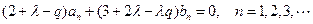 2分
2分
由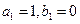 及已知递推式可求得
及已知递推式可求得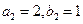 ,把它们代入上式后得方程组
,把它们代入上式后得方程组
 消去
消去 解得
解得 .…4分
.…4分
下面验证当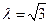 时,数列
时,数列 为等比数列.
为等比数列.
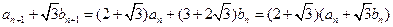
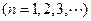 ,
,
 ,从而
,从而 是公比为
是公比为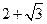 的等比数列.
的等比数列.
同理可知 是公比为
是公比为 的等比数列,于是
的等比数列,于是 为所求.……6分
为所求.……6分
(Ⅱ)由(Ⅰ)的结果得 ,
, ,解得
,解得
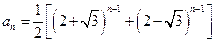 ,
,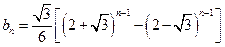 .…9分
.…9分
(Ⅲ)令数列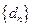 的通项公式为
的通项公式为 ,它是公比为
,它是公比为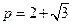 的等比数列,令其前
的等比数列,令其前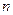 项和为
项和为 ;令数列
;令数列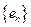 的通项公式为
的通项公式为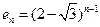 ,它是公比为
,它是公比为 的等比数列,令其前
的等比数列,令其前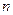 项和为
项和为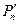 . 由第(Ⅱ)问得
. 由第(Ⅱ)问得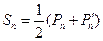 ,
,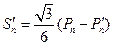 .
.
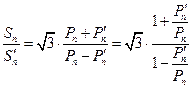 . 由于数列
. 由于数列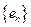 的公比
的公比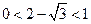 ,则
,则 .
.
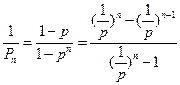 ,由于
,由于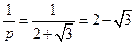 ,则
,则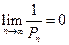 ,
,
于是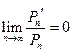 ,所以
,所以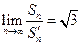 ……12
……12
 ,其中
,其中 为常数,若
为常数,若 为等比数列,则存在
为等比数列,则存在 使得
使得 .
.又
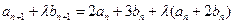
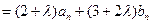 .
.所以
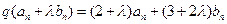 .
.由此得
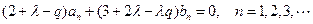 2分
2分由
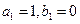 及已知递推式可求得
及已知递推式可求得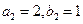 ,把它们代入上式后得方程组
,把它们代入上式后得方程组 消去
消去 解得
解得 .…4分
.…4分下面验证当
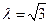 时,数列
时,数列 为等比数列.
为等比数列.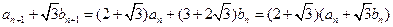
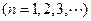 ,
, ,从而
,从而 是公比为
是公比为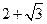 的等比数列.
的等比数列.同理可知
 是公比为
是公比为 的等比数列,于是
的等比数列,于是 为所求.……6分
为所求.……6分(Ⅱ)由(Ⅰ)的结果得
 ,
, ,解得
,解得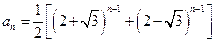 ,
,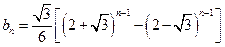 .…9分
.…9分(Ⅲ)令数列
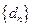 的通项公式为
的通项公式为 ,它是公比为
,它是公比为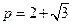 的等比数列,令其前
的等比数列,令其前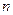 项和为
项和为 ;令数列
;令数列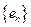 的通项公式为
的通项公式为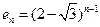 ,它是公比为
,它是公比为 的等比数列,令其前
的等比数列,令其前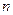 项和为
项和为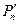 . 由第(Ⅱ)问得
. 由第(Ⅱ)问得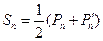 ,
,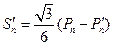 .
.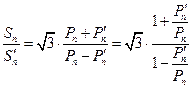 . 由于数列
. 由于数列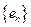 的公比
的公比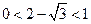 ,则
,则 .
.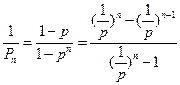 ,由于
,由于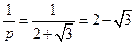 ,则
,则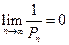 ,
,于是
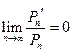 ,所以
,所以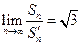 ……12
……12
练习册系列答案
 走进文言文系列答案
走进文言文系列答案
相关题目
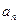 }的前n 项和为
}的前n 项和为 ,已知
,已知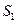 ,
,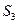 ,
,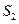 成等差数列(1)求{
成等差数列(1)求{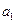 -
-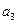 =3,求
=3,求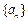 的各项为正,公比
的各项为正,公比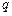 满足
满足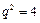 ,则
,则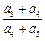 的值为()
的值为()
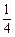
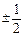
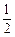
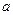 的数列
的数列 既是等差数列,又是等比数列,则这个的前
既是等差数列,又是等比数列,则这个的前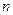 项和
项和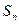 为( )
为( )