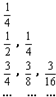题目内容

在△ABC中，a，b，c分别是A，B，C的对边，已知a，b，c成等比数列，且a2-c2=ac-bc，则
c
bsinB
的值为（　　）
A．
1
2
B．
3
2
C．
2
3
3
D．
3
由题意可得b2=ac，又a2-c2=ac-bc，
故a2-c2=b2-bc，即a2=c2+b2-bc，
由余弦定理可知a2=c2+b2-2bccosA，
故可得cosA=
1
2
，A=60°
在△ABC中，由正弦定理得sinB=
bsinA
a
，
∴
c
bsinB
=
ac
b2sinA
=
ac
acsinA
=
1
sinA
=
1
3
2
=
2
3
3
，
故选：C．
练习册系列答案
相关题目
在等比数列{an}中，已知n∈N*，且a1+a2+…+an=2n－1，那么a12+a22+…+an2等于     。
已知数列{an}满足a1=
5
2
，2an+1=3an-1．
（1）求a2，a3，a4；
（2）证明数列{an-1}是等比数列，并求{an}的通项公式．
将公比为q的等比数列{an}依次取相邻两项的乘积组成新的数列a1a2，a2a3，a3a4，…．则此数列（　　）
A．是公比为q的等比数列B．是公比为q2的等比数列
C．是公比为q3的等比数列D．不一定是等比数列
已知等比数列{an}前n项和为Sn且S5=2，S10=6，则a16+a17+a18+a19+a20等于（　　）
A．12B．16C．32D．54
给出如下一个“数阵”：如图，其中每一列成等差数列，从第三行起，每一行成等比数列，且每行的公比均相等，记第i行第j列的数为aij（i≥j，i，j∈N*）则a83=______．
已知数列1，a1，a2，9是等差数列，数列1，b1，b2，b3，9是等比数列，则
b2
a1+a2
的值为______．
已知数列{an}的前n项和Sn=2+(n-1)(
1
2
)n-1(n∈N*)，则存在数列{xn}，{yn}，使得：（　　）
A．an=xn+yn，n∈N*，其中{xn}，{yn}为等差数列
B．an=xnyn，n∈N*，其中{xn}，{yn}为等比数列
C．an=xn+yn，n∈N*，其中{xn}为等差数列，{yn}为等比数列
D．an=xnyn，n∈N*，其中{xn}为等差数列，{yn}为等比数列
在等比数列{an}中，已知a4．a7=-512，a3+a8=124，则a10=______．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网