题目内容
表面积为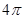 的球O与平面角为钝角的二面角的两个半平面相切于A、B两点,三角形OAB的面积
的球O与平面角为钝角的二面角的两个半平面相切于A、B两点,三角形OAB的面积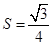 ,则球面上A、B两点间的最短距离为
,则球面上A、B两点间的最短距离为
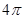 的球O与平面角为钝角的二面角的两个半平面相切于A、B两点,三角形OAB的面积
的球O与平面角为钝角的二面角的两个半平面相切于A、B两点,三角形OAB的面积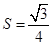 ,则球面上A、B两点间的最短距离为
,则球面上A、B两点间的最短距离为 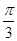
由球的表面积公式可知此球的半径为1,则由 球面上A、B两点间的最短距离为
球面上A、B两点间的最短距离为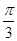 .
.
 球面上A、B两点间的最短距离为
球面上A、B两点间的最短距离为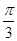 .
.
练习册系列答案
相关题目
题目内容
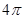 的球O与平面角为钝角的二面角的两个半平面相切于A、B两点,三角形OAB的面积
的球O与平面角为钝角的二面角的两个半平面相切于A、B两点,三角形OAB的面积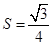 ,则球面上A、B两点间的最短距离为
,则球面上A、B两点间的最短距离为 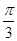
 球面上A、B两点间的最短距离为
球面上A、B两点间的最短距离为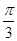 .
.