题目内容
正四面体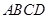 的外接球的球心为
的外接球的球心为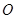 ,
,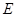 是
是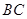 的中点,则直线
的中点,则直线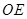 和平面
和平面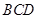 所成角的正切值为 。
所成角的正切值为 。
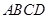 的外接球的球心为
的外接球的球心为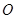 ,
,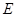 是
是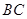 的中点,则直线
的中点,则直线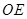 和平面
和平面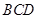 所成角的正切值为 。
所成角的正切值为 。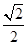
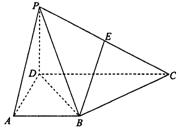
解:因为欲求直线OE与平面BCD所成角的正切值,需先找到直线在平面上的射影的位置,直线与它的射影所成角即直线OE与平面BCD所成角,根据四面体ABCD为正四面体,可得O点在平面BCD上的射影在DE上,在根据正四面体的性质,即可求∠OED的正切值.
解:设正四面体ABCD的棱长为a,连接AE,DE,
∵四面体ABCD为正四面体,E为BC的中点,
∴AE="DE="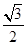 a,O点在平面ADE上,且OE等分∠AED
a,O点在平面ADE上,且OE等分∠AED
过O作OH垂直平面BCD,交平面BCD与H点,则H落在DE 上,
∴∠OED为直线OE与平面BCD所成角,然后解三角形得到。
解:设正四面体ABCD的棱长为a,连接AE,DE,
∵四面体ABCD为正四面体,E为BC的中点,
∴AE="DE="
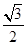 a,O点在平面ADE上,且OE等分∠AED
a,O点在平面ADE上,且OE等分∠AED过O作OH垂直平面BCD,交平面BCD与H点,则H落在DE 上,
∴∠OED为直线OE与平面BCD所成角,然后解三角形得到。

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
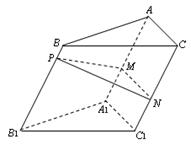
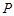 为斜三棱柱
为斜三棱柱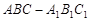 的侧棱
的侧棱 上一点,
上一点,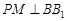 交
交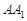 于点
于点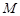 ,
,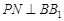 交
交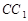 于点
于点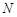 .
.
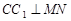 ;
;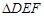 中有余弦定理:
中有余弦定理: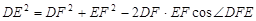 . 拓展到空间,类比三角形的余弦定理,写出斜三棱柱的三个侧面面积与其中两个侧面所成的二面角之间的关系式(只写结论,不必证明)
. 拓展到空间,类比三角形的余弦定理,写出斜三棱柱的三个侧面面积与其中两个侧面所成的二面角之间的关系式(只写结论,不必证明)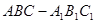 中,
中,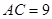 ,
,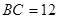 ,
,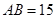 ,
,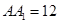 ,点D是
,点D是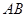 的中点.
的中点. 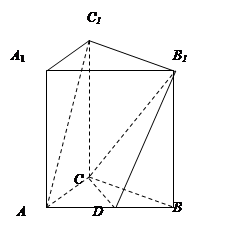
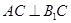 ;
;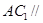 平面
平面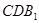 ;
; 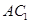 与直线
与直线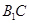 所成角的余弦值.
所成角的余弦值. 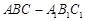 中,已知
中,已知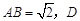 在棱
在棱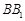 上,且
上,且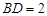 ,若
,若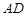 与平面
与平面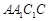 所成的角为
所成的角为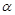 ,则
,则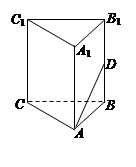
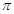 cm2
cm2 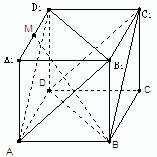
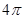 的球O与平面角为钝角的二面角的两个半平面相切于A、B两点,三角形OAB的面积
的球O与平面角为钝角的二面角的两个半平面相切于A、B两点,三角形OAB的面积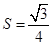 ,则球面上A、B两点间的最短距离为
,则球面上A、B两点间的最短距离为