题目内容
10.已知复数x2-6x+5+(x-2)i在复平面内对应的点在第三象限,则实数x的取值范围为(1,2).分析 利用复数的点所在象限,推出不等式,求解即可.
解答 解:复数x2-6x+5+(x-2)i在复平面内对应的点在第三象限,
可得$\left\{\begin{array}{l}{x}^{2}-6x+5<0\\ x-2<0\end{array}\right.$,解得x∈(1,2).
故答案为:(1,2).
点评 本题考查复数的几何意义,不等式的解法,考查计算能力.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
18.现有六本书,其中两本相同,其余四本各不相同,分成三堆,每堆两本,则不同的分法的种数为( )
| A. | 9种 | B. | 12种 | C. | 15种 | D. | 18种 |
5.若复数$\frac{1+bi}{2+i}$是纯虚数(i是虚数单位,b是实数),则b=( )
| A. | -2 | B. | -$\frac{1}{2}$ | C. | $\frac{1}{2}$ | D. | 2 |
15.下列函数中,既是偶函数又存在零点的是( )
| A. | y=cosx | B. | y=sinx | C. | y=lnx | D. | y=x2+1 |
19.不等式|x-1|-|x-5|<2的解集是( )
| A. | (-∞,4) | B. | (-∞,1) | C. | (1,4) | D. | (1,5) |
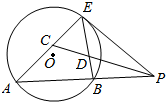 如图,已知PE为圆eO的切线,切点为E,割线PBA交eO于A、B两点,C为AE上一点,且∠CPE=∠CPA.
如图,已知PE为圆eO的切线,切点为E,割线PBA交eO于A、B两点,C为AE上一点,且∠CPE=∠CPA.