题目内容
20.已知直线l:x-y+1=0与抛物线C:x2=2y交于A,B两点,点P为直线l上一动点,M,N是抛物线C上两个动点,若$\overrightarrow{MN}∥\overrightarrow{AB}$,$|\overrightarrow{MN}|<|\overrightarrow{AB}|$,则△PMN的面积的最大值为1.分析 设MN:x-y+c=0(-$\frac{1}{2}$<c<1),求出P到MN的距离,|MN|,可得三角形的面积,再用导数法求解即可.
解答 解:设MN:x-y+c=0(-$\frac{1}{2}$<c<1),则P到MN的距离为$\frac{|c-1|}{\sqrt{2}}$,
x-y+c=0与x2=2y联立,可得x2-2x-2c=0,∴x=1±$\sqrt{2c+1}$,
∴|MN|=$\sqrt{2}•$2$\sqrt{2c+1}$,
∴△PMN的面积=$\frac{1}{2}$•$\sqrt{2}•$2$\sqrt{2c+1}$•$\frac{|c-1|}{\sqrt{2}}$=$\sqrt{(2c+1)(c-1)^{2}}$
令y=(2c+1)(c-1)2,∴y′=6c(c-1)
∴(-$\frac{1}{2}$,0),y′>0,(0,1)上,y′<0
∴c=0时,y取得最大值1,
∴△PMN的面积的最大值为1.
故答案为:1.
点评 本题考查三角形面积的计算,考查直线与抛物线的位置关系,考查导数知识的运用,确定三角形的面积是关键.

练习册系列答案
相关题目
3.已知m=loga$\frac{3}{2}$+loga2,n=logb9-logb3,若m<n,则下列结论中,不可能成立的是( )
| A. | 0<b<a<1 | B. | 0<a<b<1 | C. | a>b>1 | D. | 0<a<1<b |
8.已知全集为R,f(x)=$\frac{1}{\sqrt{lo{g}_{2}x-1}}$的定义域为集合A,x2-2x-3≥0的解集为集合B,则A∩(∁MB)=( )
| A. | (0,3) | B. | [2,3) | C. | (2,3) | D. | [3,+∞) |
15.命题“?x≥0,|x|+x≥0”的否定是( )
| A. | ?x≥0,|x0|+x0<0 | B. | ?x<0,|x|+x≥0 | C. | ?x0≥0,|x0|+x0<0 | D. | ?x0<0,|x|+x≥0 |
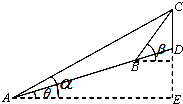 如图,一山顶有一信号塔CD(CD所在的直线与地平面垂直),在山脚A处测得塔尖C的仰角为α,沿倾斜角为θ的山坡向上前进l米后到达B处,测得C的仰角为β.
如图,一山顶有一信号塔CD(CD所在的直线与地平面垂直),在山脚A处测得塔尖C的仰角为α,沿倾斜角为θ的山坡向上前进l米后到达B处,测得C的仰角为β.