题目内容
已知f(x)=x2-2017x+8052+|x2-2017x+8052|,则f(1)+f(2)+f(3)+…+f(2013)= .
24136
由于g(x)=x2-2017x+8052=(x-4)(x-2013),∴f(4)=f(2013)=0.
∴x∈(4,2013)时g(x)<0,f(x)=0,∴f(5)=f(6)=…=f(2012)=0,故所求为f(1)+f(2)+f(3)=2[g(1)+g(2)+g(3)]=24136.
∴x∈(4,2013)时g(x)<0,f(x)=0,∴f(5)=f(6)=…=f(2012)=0,故所求为f(1)+f(2)+f(3)=2[g(1)+g(2)+g(3)]=24136.

练习册系列答案
 时刻准备着暑假作业原子能出版社系列答案
时刻准备着暑假作业原子能出版社系列答案 暑假衔接教材期末暑假预习武汉出版社系列答案
暑假衔接教材期末暑假预习武汉出版社系列答案 假期作业暑假成长乐园新疆青少年出版社系列答案
假期作业暑假成长乐园新疆青少年出版社系列答案
相关题目
 假定该产品产销平衡,根据上述统计规律求:
假定该产品产销平衡,根据上述统计规律求: 是
是 上的增函数,
上的增函数, ,已知
,已知 .
. 在
在 单调递增,求实数
单调递增,求实数 的取值范围;
的取值范围;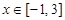 时,
时, ,求实数
,求实数 )元.
)元.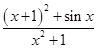 的最大值为M,最小值为m,则M+m= .
的最大值为M,最小值为m,则M+m= .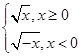 若f(a)+f(-1)=2,则a=( )
若f(a)+f(-1)=2,则a=( )