题目内容
某银行准备新设一种定期存款业务,经预算,存款量与存款利率的平
方成正比,比例系数为k(k>0),贷款的利率为0.048,假设银行吸收的存款能全部放贷出去.若存款利率为x(x∈(0,0.048)),则x为多少时,银行可获得最大收益 ( ).
方成正比,比例系数为k(k>0),贷款的利率为0.048,假设银行吸收的存款能全部放贷出去.若存款利率为x(x∈(0,0.048)),则x为多少时,银行可获得最大收益 ( ).
| A.0.016 | B.0.032 |
| C.0.024 | D.0.048 |
B
依题意:存款量是kx2,银行应支付的利息是kx3,贷款的收益是0.048kx2,其中x∈(0,0.048).
所以银行的收益是y=0.048kx2-kx3(0<x<0.048),
由于y′=0.096kx-3kx2,令y′=0得x=0.032或x=0(舍去),
又当0<x<0.032时,y′>0;
当0.032<x<0.048时,y′<0,
所以当x=0.032时,y取得最大值,即当存款利率为0.032时,银行可获得最大收益.
所以银行的收益是y=0.048kx2-kx3(0<x<0.048),
由于y′=0.096kx-3kx2,令y′=0得x=0.032或x=0(舍去),
又当0<x<0.032时,y′>0;
当0.032<x<0.048时,y′<0,
所以当x=0.032时,y取得最大值,即当存款利率为0.032时,银行可获得最大收益.

练习册系列答案
相关题目
 (单位:元)与上市时间
(单位:元)与上市时间 (单位:天)的数据如下:
(单位:天)的数据如下: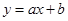 ;②
;② ;③
;③ .
. 上的函数
上的函数 满足:对于任意的
满足:对于任意的 ,都有
,都有 ,且
,且 时,有
时,有 ,
,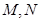 ,则
,则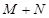 的值为( )
的值为( ) 与
与
 与
与
 与
与
 与
与