题目内容
一次函数 是
是 上的增函数,
上的增函数, ,已知
,已知 .
.
(1)求 ;
;
(2)若 在
在 单调递增,求实数
单调递增,求实数 的取值范围;
的取值范围;
(3)当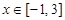 时,
时, 有最大值
有最大值 ,求实数
,求实数 的值.
的值.
 是
是 上的增函数,
上的增函数, ,已知
,已知 .
.(1)求
 ;
;(2)若
 在
在 单调递增,求实数
单调递增,求实数 的取值范围;
的取值范围;(3)当
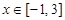 时,
时, 有最大值
有最大值 ,求实数
,求实数 的值.
的值.(1) ;(2)
;(2) ;(3)
;(3) 或
或 .
.
 ;(2)
;(2) ;(3)
;(3) 或
或 .
.试题分析:(1)先设
 ,然后由
,然后由 恒成立得方程组
恒成立得方程组 ,求解方程组即可,注意取
,求解方程组即可,注意取 的解;(2)由(1)得
的解;(2)由(1)得 ,根据二次函数的图像与性质可知,要使
,根据二次函数的图像与性质可知,要使 在
在 单调递增,只须该函数的对称轴大于或于1即可;(3)这是二次函数中定区间,而轴不定的最值问题,结合函数的图像,分对称轴在定区间的中点的左边、对称轴在定区间的中点的右边两种情况进行分类求解即可.
单调递增,只须该函数的对称轴大于或于1即可;(3)这是二次函数中定区间,而轴不定的最值问题,结合函数的图像,分对称轴在定区间的中点的左边、对称轴在定区间的中点的右边两种情况进行分类求解即可.试题解析:(1)∵
 是
是 上的增函数,∴设
上的增函数,∴设 1分
1分
∴
 3分
3分解得
 或
或 (不合题意舍去) 5分
(不合题意舍去) 5分∴
 6分
6分(2)
 7分
7分对称轴
 ,根据题意可得
,根据题意可得 8分
8分解得

∴
 的取值范围为
的取值范围为 9分
9分(3)①当
 时,即
时,即 时
时 ,解得
,解得 ,符合题意 11分
,符合题意 11分②当
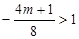 时,即
时,即 时
时 ,解得
,解得 ,符合题意 13分
,符合题意 13分由①②可得
 或
或 14分.
14分.
练习册系列答案
 中考利剑中考试卷汇编系列答案
中考利剑中考试卷汇编系列答案 教育世家状元卷系列答案
教育世家状元卷系列答案
相关题目
 <-1.
<-1. =C,则称函数f(x)在D上的几何平均数为C.已知f(x)=x3,x∈[1,2],则函数f(x)=x3在[1,2]上的几何平均数为( )
=C,则称函数f(x)在D上的几何平均数为C.已知f(x)=x3,x∈[1,2],则函数f(x)=x3在[1,2]上的几何平均数为( )
 函数f(x) =max{|x+1|,|x-2|}(x∈R)的最小值是( )
函数f(x) =max{|x+1|,|x-2|}(x∈R)的最小值是( )

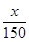 +2是否符合公司要求的奖励函数模型,并说明原因;
+2是否符合公司要求的奖励函数模型,并说明原因; 作为奖励函数模型,试确定最小的正整数a的值.
作为奖励函数模型,试确定最小的正整数a的值. 的定义域和值域都是
的定义域和值域都是 ,其对应关系如下表所示,则
,其对应关系如下表所示,则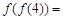 .
.