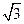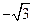题目内容
已知函数f(x)(x∈R)满足f(1)=1,且f(x)的导函数f′(x)>
,则f(x)-
-
>0的解集为______.
| 1 |
| 3 |
| x |
| 3 |
| 2 |
| 3 |
∵函数f′(x)>
,
令g(x)=f(x)-
-
,
则f′(x)=f′(x)-
>0.
∴函数g(x)在R上单调递增,
又g(1)=f(1)-
-
=1-1=0,
∴当x>1时,g(x)>g(1)=0.
∴f(x)-
-
>0的解集为(1,+∞).
故答案为:(1,+∞).
| 1 |
| 3 |
令g(x)=f(x)-
| x |
| 3 |
| 2 |
| 3 |
则f′(x)=f′(x)-
| 1 |
| 3 |
∴函数g(x)在R上单调递增,
又g(1)=f(1)-
| 1 |
| 3 |
| 2 |
| 3 |
∴当x>1时,g(x)>g(1)=0.
∴f(x)-
| x |
| 3 |
| 2 |
| 3 |
故答案为:(1,+∞).

练习册系列答案
相关题目
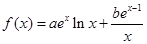 ,曲线
,曲线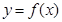 在点
在点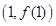 处的切线为
处的切线为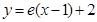 .
.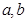 ;
;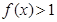 .
.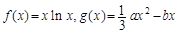 ,其中a,b∈R
,其中a,b∈R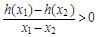 成立,试用a表示出b的取值范围;
成立,试用a表示出b的取值范围;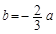 时,若
时,若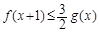 对x∈[0,+∞)恒成立,求a的最小值.
对x∈[0,+∞)恒成立,求a的最小值.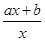 ex,a,b
ex,a,b R,且a>0.
R,且a>0.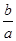 的取值范围.
的取值范围.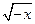 (x
(x 0)的反函数是
0)的反函数是 (x
(x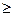 0) (B)
0) (B)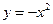 (x
(x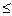 0) (D)
0) (D)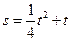 ,求何时质点的速度为
,求何时质点的速度为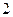 。
。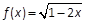 ,则
,则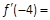 ( ).
( ).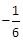
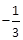
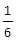
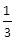
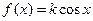 的图象经过点P(
的图象经过点P( 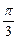 , 1) , 则函数图象上过点P的切线斜率等于 ( )
, 1) , 则函数图象上过点P的切线斜率等于 ( )