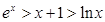题目内容
证明不等式ex>x+1>㏑x,x>0
见解析
试题分析:要证明该不等式得分两步,首先证明
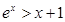 ,设出
,设出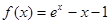 ,只需证明
,只需证明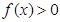 即可,所以求导,根据
即可,所以求导,根据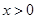 ,判断单调性,从而得出
,判断单调性,从而得出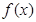 的最小值,证明.同理证明
的最小值,证明.同理证明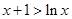 .
.试题解析:①令
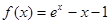 ,
,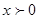
则
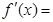
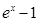
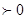 ,所以
,所以 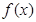 在
在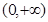 上单调递增。
上单调递增。故对任意
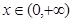 ,有
,有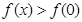
而
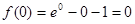 ,所以
,所以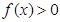
即
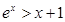
②令
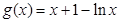 ,
,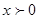 ,
,则
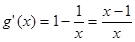
令
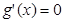 ,得
,得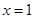
当
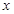 变化时,
变化时,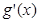 ,
,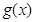 的变化情况如下表:
的变化情况如下表: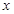 | 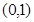 | 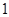 | 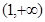 |
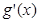 | - | 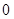 | 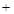 |
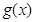 |  ↘ ↘ | 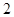 | ↗ |
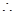

即对任意
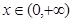 有
有 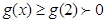
所以
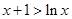
综上当
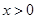 时,有
时,有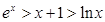

练习册系列答案
相关题目
题目内容
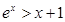 ,设出
,设出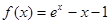 ,只需证明
,只需证明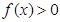 即可,所以求导,根据
即可,所以求导,根据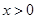 ,判断单调性,从而得出
,判断单调性,从而得出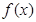 的最小值,证明.同理证明
的最小值,证明.同理证明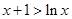 .
.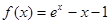 ,
,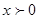
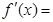
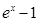
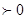 ,所以
,所以 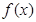 在
在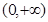 上单调递增。
上单调递增。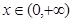 ,有
,有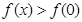
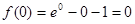 ,所以
,所以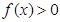
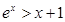
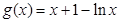 ,
,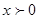 ,
,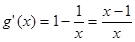
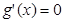 ,得
,得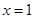
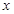 变化时,
变化时,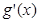 ,
,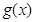 的变化情况如下表:
的变化情况如下表: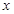 | 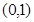 | 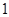 | 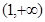 |
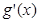 | - | 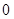 | 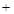 |
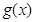 |  ↘ ↘ | 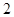 | ↗ |
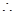

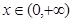 有
有 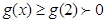
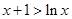
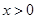 时,有
时,有