题目内容
【题目】如图，在矩形ABCD和矩形ABEF中，
，
，矩形ABEF可沿AB任意翻折.
（1）求证：当点F，A，D不共线时，线段MN总平行于平面ADF.
（2）“不管怎样翻折矩形ABEF，线段MN总与线段FD平行”这个结论正确吗？如果正确，请证明；如果不正确，请说明能否改变个别已知条件使上述结论成立，并给出理由.
【答案】（1）证明见解析；（2）这个结论不正确.要使上述结论成立，M，N应分别为AE和DB的中点，理由见解析
【解析】
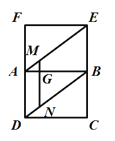
（1）在平面图形中，连接MN与AB交于点G，在平面图形中可证
，当点F，A，D不共线时，
，
，可证
平面ADF，
平面ADF，从而有平面
平面ADF，即可证明结论；
（2）这个结论不正确.要使上述结论成立，M，N应分别为AE和DB的中点.
当点F，A，D共线时，由（1）得
；当点F，A，D不共线时，平面
平面FDA，则要使，满足FD与AN共面，只要FM与DN相交即可，可证交点只能为点B，得出只有M，N分别为AE，DB的中点才满足.
（1）证明：在平面图形中，连接MN，与AB交于点G.
∵四边形ABCD和四边形ABEF都是矩形，
，
∴
且
，
∴四边形ADBE是平行四边形，∴
.
又
，∴四边形ADNM是平行四边形，∴.
当点F，A，D不共线时，如图，，，
平面
，
平面，所以平面ADF，
同理平面ADF，又
，
平面
，∴平面平面ADF.
又
平面GNM，∴
平面ADF.
故当点F，A，D不共线时，线段MN总平行于平面FA D.
（2）解：这个结论不正确.
要使上述结论成立，M，N应分别为AE和DB的中点.理由如下：
当点F，A，D共线时，由（1）得.
当点F，A，D不共线时，如图，
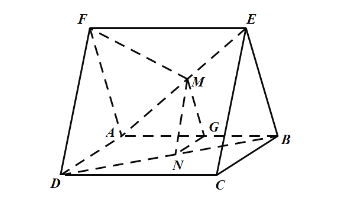
由（1）知平面平面FDA，则要使总成立，
根据面面平行的性质定理，只要FD与
共面即可.
若要使FD与共面，连接FM，只要FM与DN相交即可，
∵
平面ABEF，
平面ABCD，
平面
平面
，
∴若FM与DN相交，则交点只能为点B，
由于四边形
为平行四边形，
与
的交点
为的中点，
则只有M，N分别为AE，DB的中点才满足.
由
，
可知它们确定一个平面，即F，D，N，M四点共面.
∵平面
平面
，
平面平面
，
平面平面FDA，∴.
