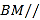题目内容
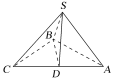
【题目】如图,在正方体![]() 中.
中.

(1)求证:平面![]() 平面
平面![]() ;
;
(2)试找出体对角线![]() 与平面
与平面![]() 和平面
和平面![]() 的交点
的交点![]() ,并证明:
,并证明:![]() .
.
【答案】(1)见解析(2)见解析
【解析】
(1)先由平行四边形得线线平行,由线面平行判定定理再证得线面平行,找到两条相交线运用面面平行的判定定理证明结果.
(2)连接辅助线,由中点构造出三角形的中位线,这样证明得到线段相等,运用同样的方法来证明另外两条线段相等,即得证三条线段相等.
解析 (1)证明:因为在正方体![]() 中,
中,![]() ,
,
所以四边形![]() 是平行四边形,所以
是平行四边形,所以![]() .
.
又因为![]() 平面
平面![]() ,
,![]() 平面
平面![]() ,所以
,所以![]() 平面
平面![]() .
.
同理![]() 平面
平面![]() .又因为
.又因为![]() ,
,![]() 平面
平面![]() ,
,![]() 平面
平面![]() ,所以平面
,所以平面![]() 平面
平面![]() .
.
(2)如图,连接![]() 交
交![]() 于点
于点![]() ,连接
,连接![]() 与
与![]() 交于点E.又因为
交于点E.又因为![]() 平面
平面![]() ,所以点E也在平面
,所以点E也在平面![]() 内,所以点E就是
内,所以点E就是![]() 与平面
与平面![]() 的交点;连接
的交点;连接![]() 交
交![]() 于点O,连接
于点O,连接![]() 与
与![]() 交于点F,则点F就是
交于点F,则点F就是![]() 与平面
与平面![]() 的交点.
的交点.
下面证明![]() :
:
因为平面![]() 平面
平面![]() ,平面
,平面![]() 平面
平面![]() ,
,
平面![]() 平面
平面![]() ,所以
,所以![]() .在
.在![]() 中,
中,![]() 是
是![]() 的中点,所以E是
的中点,所以E是![]() 的中点,即
的中点,即![]() ;同理可证
;同理可证![]() ,所以F是
,所以F是![]() 的中点,即
的中点,即![]() ,所以
,所以![]() .
.


练习册系列答案
 同步练习河南大学出版社系列答案
同步练习河南大学出版社系列答案 同步练习西南师范大学出版社系列答案
同步练习西南师范大学出版社系列答案 补充习题江苏系列答案
补充习题江苏系列答案 学练快车道口算心算速算天天练系列答案
学练快车道口算心算速算天天练系列答案
相关题目