题目内容
【题目】某厂生产的某种零件的尺寸![]() 大致服从正态分布
大致服从正态分布![]() ,且规定尺寸
,且规定尺寸![]() 为次品,其余的为正品.生产线上的打包机自动把每5件零件打包成1箱,然后进入销售环节,若每销售一件正品可获利50元,每销售一件次品亏损100元.现从生产线生产的零件中抽样20箱做质量分析,作出的频率分布直方图如下:
为次品,其余的为正品.生产线上的打包机自动把每5件零件打包成1箱,然后进入销售环节,若每销售一件正品可获利50元,每销售一件次品亏损100元.现从生产线生产的零件中抽样20箱做质量分析,作出的频率分布直方图如下:
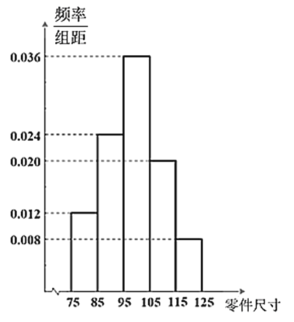
(1)估计生产线生产的零件的次品率及零件的平均尺寸;
(2)从生产线上随机取一箱零件,求这箱零件销售后的期望利润及不亏损的概率.
【答案】(1)0.20;98.8(2)![]()
【解析】
(1)求出![]() 的值,即可得到次品的尺寸范围,根据频率分布图求出次品率,并求出各组的频率,按照平均数公式即可求解;
的值,即可得到次品的尺寸范围,根据频率分布图求出次品率,并求出各组的频率,按照平均数公式即可求解;
(2)设生产线上的一箱零件(5件)中的正品数为![]() ,则
,则![]() ,将利润表示为
,将利润表示为![]() 的函数,由二项分布的期望公式和期望的性质,求出利润的期望;要使销售不亏损,5件产品中至少要有4件正品,根据独立重复试验的概率公式,即可求解.
的函数,由二项分布的期望公式和期望的性质,求出利润的期望;要使销售不亏损,5件产品中至少要有4件正品,根据独立重复试验的概率公式,即可求解.
(1)次品的尺寸范围![]() ,
,
即![]() ,即
,即![]() ,
,
故生产线生产的产品次品率为:![]()
生产线生产的产品平均尺寸为:
![]()
(2)设生产线上的一箱零件(5件)中的正品数为![]() ,
,
正品率为![]() ,故
,故![]() ,
,![]()
设销售生产线上的一箱零件获利为![]() 元,
元,
则![]()
![]() (元)
(元)
设事件![]() :销售生产线上的一箱零件不亏损,则
:销售生产线上的一箱零件不亏损,则
![]()
![]() ,
,
答:生产线生产的零件的次品率为0.2,零件的平均尺寸为98.8,
这箱零件销售后的期望利润为100元,不亏损的概率为![]() .
.

【题目】某花店每天以每枝![]() 元的价格从农场购进若干枝玫瑰花,然后以每枝
元的价格从农场购进若干枝玫瑰花,然后以每枝![]() 元价格出售,如果当天卖不完,剩下的玫瑰花作垃圾处理.
元价格出售,如果当天卖不完,剩下的玫瑰花作垃圾处理.
(1)若花店一天购进![]() 枝玫瑰花,求当天的利润
枝玫瑰花,求当天的利润![]() (单位:元)关于当天需求量
(单位:元)关于当天需求量![]() (单位:枝,
(单位:枝, ![]() )的函数解析式;
)的函数解析式;
(2)花店记录了![]() 天玫瑰花的日需求量(单位:枝),整理得下表:
天玫瑰花的日需求量(单位:枝),整理得下表:
日需求量 |
|
|
|
|
|
|
|
频数 |
|
|
|
|
|
|
|
以![]() 天的各需求量的频率作为各需求量发生的概率.
天的各需求量的频率作为各需求量发生的概率.
![]() 若花店一天购进
若花店一天购进![]() 枝玫瑰花,
枝玫瑰花, ![]() 表示当天的利润(单位:元),求
表示当天的利润(单位:元),求![]() 的分布列, 数学期望及方差;
的分布列, 数学期望及方差;
![]() 若花店一天购进
若花店一天购进![]() 枝或
枝或![]() 枝玫瑰花,你认为应购进
枝玫瑰花,你认为应购进![]() 枝还是
枝还是![]() 枝?请说明理由.
枝?请说明理由.