题目内容
【题目】一个人上台阶可以一次上1级台阶,也可以一次上3级台阶,或者一次上4级台阶.若这个人上![]() 级台阶总共有
级台阶总共有![]() 种走法,证明
种走法,证明![]() 为平方数.
为平方数.
【答案】见解析
【解析】
若最后一步上1级台阶,前面有![]() 种走法;
种走法;
若最后一步上3级台阶,前面有![]() 种走法;
种走法;
若最后一步上4级台阶,前面有![]() 种走法.
种走法.
于是,![]() .
.
又![]() ,
,![]() ,
,![]() ,
,![]() ,故有足够多的初始条件使得
,故有足够多的初始条件使得![]() 能被唯一确定.
能被唯一确定.
以下用数学归纳法证明两个结论.
(1)![]() .①
.①
当![]() 时,
时,![]() ,式①显然成立.
,式①显然成立.
设小于![]() 时,对所有的奇数项均有式①成立.
时,对所有的奇数项均有式①成立.
则![]() 时,有
时,有![]() (由递推式)
(由递推式)
![]() (由归纳假设).故
(由归纳假设).故![]() 时式①也成立.
时式①也成立.
综上,![]() 时式①成立.
时式①成立.
(2)![]() .②
.②
当![]() 时,
时,![]() ,式②显然成立.
,式②显然成立.
设![]() 时,有
时,有![]() 成立.
成立.
当![]() 时,
时,
![]()
![]()
![]()
![]() .
.
因此,![]() .
.
若![]() 为平方数,由于
为平方数,由于![]() 为整数,则必有
为整数,则必有![]() 为平方数.
为平方数.
又![]() 为平方数,由数学归纳法,易得
为平方数,由数学归纳法,易得![]() 为平方数.
为平方数.

练习册系列答案
相关题目
【题目】在一次飞机航程中,调查男女晕机情况,在80名男乘客中有10人晕机,70人不晕机.在30名女乘客中有10人晕机,20人不晕机
(1)请根据题设数据列出![]() 列联表
列联表
晕机 | 不晕机 | 总计 | |
男 | |||
女 | |||
总计 |
(2)是否有![]() 把握认为“是否晕机与性别有关”.
把握认为“是否晕机与性别有关”.
附:![]()
| 0.050 | 0.025 | 0.010 |
| 3.841 | 5.024 | 6.635 |
【题目】某医院用光电比色计检查尿汞时,得尿汞含量(毫克/升)与消光系数如下表:
尿汞含量 | 2 | 4 | 6 | 8 | 10 |
消光系数 | 64 | 138 | 205 | 285 | 360 |
(1)作散点图;
(2)如果![]() 与
与![]() 之间具有线性相关关系,求回归线直线方程;
之间具有线性相关关系,求回归线直线方程;
(3)估计尿汞含量为9毫克/升时消光系数.
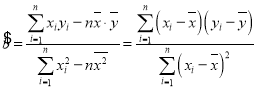 ,
,![]() .
.
参考数据:![]() ,
,![]() .
.