题目内容
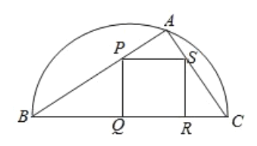
【题目】如图，某园林单位准备绿化一块直径为BC的半圆形空地，
外的地方种草，的内接正方形PQRS为一水池，其余的地方种花.若
，
，设的面积为
，正方形PQRS的面积为
.
（1）用a，
表示和；
（2）当a为定值，变化时，求
的最小值，及此时的值.
【答案】（1）
；
（2）当
时，
的值最小，最小值为
【解析】
（1）利用已知条件，根据锐角三角形中正余弦的利用，即可表示出
和
；
（2）根据题意，将表示为
的函数，利用倍角公式对函数进行转化，利用换元法，借助对勾函数的单调性，从而求得最小值.
（1）在
中，
，
所以
；
设正方形的边长为x，则
，
，
由
，得
，
解得
；
所以
；
（2）
，
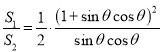
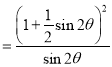
令
，因为
，
所以
，则
，
所以
；
设
，
根据对勾函数的单调性可知，
在
上单调递减，
因此当
时，
有最小值
，
此时
，解得；
所以当时，的值最小，最小值为.
练习册系列答案
名校课堂系列答案
相关题目
