题目内容
已知p：关于x的方程x2+2x+m-1=0没有实根，q：不等式4x2+4（m-2）x+1＞0的解集为R，
（1）若￢q为假命题，求m的取值范围；
（2）若p∨q为真命题，p∧q为假命题，求m的取值范围．
（1）若￢q为假命题，求m的取值范围；
（2）若p∨q为真命题，p∧q为假命题，求m的取值范围．
（1）根据题意q为真命题，2分
又∵4x2+4（m-2）x+1＞0 的解集为R，∴△=16（m-2）2-16＜0⇒1＜m＜3
∴m∈{m|1＜m＜3}.4分
（2）∵关于x的方程x2+2x+m-1=0没有实根，
∴△=4-4（m-1）＜0⇒m＞2，∴p为真命题，m∈{m|m＞2}.6分
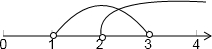
∵p∨q为真命题，p∧q为假命题，∴P、q一真一假，
∴m≥3或1＜m≤2
故m∈{m|1＜m≤2或m≥3}12分
又∵4x2+4（m-2）x+1＞0 的解集为R，∴△=16（m-2）2-16＜0⇒1＜m＜3
∴m∈{m|1＜m＜3}.4分
（2）∵关于x的方程x2+2x+m-1=0没有实根，
∴△=4-4（m-1）＜0⇒m＞2，∴p为真命题，m∈{m|m＞2}.6分
∵p∨q为真命题，p∧q为假命题，∴P、q一真一假，
∴m≥3或1＜m≤2
故m∈{m|1＜m≤2或m≥3}12分
练习册系列答案
相关题目
