题目内容
如图，三棱锥A-BCD中，AB⊥AD，AC⊥AD，∠BAC=θ（0＜θ≤
），且AB=AC=AD=2，E、F分别为AC、BD的中点，则EF的最大值为______．
| π |
| 2 |
过F作FG⊥AB，垂足为G，连接GE，
∵AD⊥AB，
∴AD∥FG，∴G为AB的中点，
∴FG=1，AG=1，
∵E为AC的中点，∴AE=1，∠BAC=θ，
∴EG=
∵AD⊥平面ABC，∴FG⊥平面ABC，
在Rt△FGE中，EF=
=
=
，
∵0＜θ≤
，∴EF≤
．
故答案是
．
∵AD⊥AB，
∴AD∥FG，∴G为AB的中点，
∴FG=1，AG=1，
∵E为AC的中点，∴AE=1，∠BAC=θ，
∴EG=
| 12+12-2×1×1×cosθ |
∵AD⊥平面ABC，∴FG⊥平面ABC，
在Rt△FGE中，EF=
| EG2+FG2 |
| 2-2cosθ+1 |
| 3-2cosθ |
∵0＜θ≤
| π |
| 2 |
| 3 |
故答案是
| 3 |
练习册系列答案
口算题卡加应用题集训系列答案
综合自测系列答案
相关题目
及其三视图如图所示，平行于棱
的平面分别交四面体的棱
于点
.
是矩形.
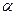和共面的直线
、
下列命题中真命题是
则
B．若
则
则
与