题目内容
5.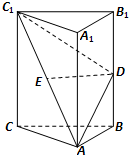 如图,在直三棱柱ABC-A1B1C1中,AB=BC,D,E分别为BB1,AC1的中点.
如图,在直三棱柱ABC-A1B1C1中,AB=BC,D,E分别为BB1,AC1的中点.(1)证明:DE⊥平面ACC1A1;
(2)设AA1=AC=$\sqrt{2}$AB,求二面角A1-AD-C1的大小.
分析 方法1:(综合法)
(1)设O为AC中点,连结EO,BO,证明EO∥BD,然后证明OB⊥平面ACC1A1,推出DE⊥平面ACC1A1.
(2)连结A1E,过点E作EF⊥AD,垂足为F,连结A1F.说明A1FE为二面角A1-AD-C1的平面角.然后在三角形中求解二面角A1-AD-C1的大小为60°.
方法2:(坐标法)
(1)设O为AC中点,以$\overrightarrow{OA},\overrightarrow{OB},\overrightarrow{OE}$为正交基底建立如图的空间直角坐标系O-xyz,证明$\overrightarrow{OA}•\overrightarrow{ED}=0$,$\overrightarrow{A{A_1}}•\overrightarrow{ED}=0$,推出ED⊥平面ACC1A1.
(2)求出平面A1AD的法向量,平面C1AD的法向量,利用空间向量的数量积求解二面角A1-AD-C1的大小即可.
解答 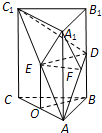 解:方法1:(综合法)
解:方法1:(综合法)
(1)设O为AC中点,连结EO,BO,则EO∥CC1,且$EO=\frac{1}{2}C{C_1}$,…(1分)
又CC1∥BB1,且CC1=BB1,
∴EO∥BD,且EO=BD,即四边形EOBD为平行四边形,
∴ED∥OB,…(3分)
∵AA1⊥底面ABC,OB?底面ABC,∴AA1⊥OB,…(4分)
∵AB=BC,O为AC中点,
∴OB⊥AC,又AC∩AA1=A,…(5分)
∴OB⊥平面ACC1A1,故DE⊥平面ACC1A1.…(6分)
(2)连结A1E,过点E作EF⊥AD,垂足为F,连结A1F.…(7分)
由$A{A_1}=AC=\sqrt{2}AB$可知ACC1A1为正方形,则A1E⊥AC1,
∵DE⊥平面ACC1A1,又A1E?平面ACC1A1,
∴A1E⊥DE,又AC1∩DE=E,
∴A1E⊥平面ADC1,又AD?平面ADC1,…(9分)
∴A1E⊥AD,又EF⊥AD,A1E∩EF=E,
∴AD⊥平面A1EF,又A1F?平面A1EF,
∴A1F⊥AD,…(11分)
∴∠A1FE为二面角A1-AD-C1的平面角. …(12分)
不妨设AA1=2,则AC=2,$AB=\sqrt{2}$,ED=OB=1,$EF=\frac{AE×ED}{AD}=\frac{{\sqrt{2}}}{{\sqrt{3}}}$,
∴$tan∠{A_1}FE=\frac{{{A_1}E}}{EF}=\sqrt{3}$,
所以二面角A1-AD-C1的大小为60°. …(14分)
方法2:(坐标法)
(1)设O为AC中点,由AB=BC知OB⊥AC,以$\overrightarrow{OA},\overrightarrow{OB},\overrightarrow{OE}$为正交基底建立如图的空间直角坐标系O-xyz,
设A(a,0,0),B(0,b,0),E(0,0,c),则A1(a,0,2c),D(0,b,c),
∴$\overrightarrow{OA}=(a,0,0)$,$\overrightarrow{A{A_1}}=(0,0,2c)$,$\overrightarrow{ED}=(0,b,0)$,
∴$\overrightarrow{OA}•\overrightarrow{ED}=0$,$\overrightarrow{A{A_1}}•\overrightarrow{ED}=0$,
∴ED⊥OA,ED⊥AA1,又OA∩AA1=A,
故ED⊥平面ACC1A1.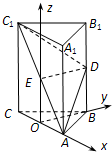
(2)由$A{A_1}=AC=\sqrt{2}AB$不妨设A(1,0,0),
则B(0,1,0),C(-1,0,0),E(0,0,1),A1(1,0,2),D(0,1,1),
∴$\overrightarrow{BC}=(-1,-1,0)$,$\overrightarrow{AB}=(-1,1,0)$,$\overrightarrow{A{A_1}}=(0,0,2)$,
∴$\overrightarrow{BC}•\overrightarrow{AB}=0$,$\overrightarrow{BC}•\overrightarrow{A{A_1}}=0$,即BC⊥AB,BC⊥AA1,又AB∩AA1=A,
∴BC⊥平面A1AD,故平面A1AD的法向量可取$\overrightarrow{BC}=(-1,-1,0)$.
又$\overrightarrow{EC}=(-1,0,-1)$,$\overrightarrow{AE}=(-1,0,1)$,$\overrightarrow{ED}=(0,1,0)$,
∴$\overrightarrow{EC}•\overrightarrow{AE}=0$,$\overrightarrow{EC}•\overrightarrow{ED}=0$,即EC⊥AE,EC⊥ED,又AE∩ED=E,
∴EC⊥平面C1AD,故平面C1AD的法向量可取$\overrightarrow{EC}=(-1,0,-1)$.
∵$cos<\overrightarrow{EC},\overrightarrow{BC}>=\frac{{\overrightarrow{EC}•\overrightarrow{BC}}}{{|\overrightarrow{EC}||\overrightarrow{BC}|}}=\frac{1}{{\sqrt{2}×\sqrt{2}}}=\frac{1}{2}$,
∴所以二面角A1-AD-C1的大小为60°.…(14分)
点评 本题考查直线与平面垂直的判定定理,二面角的平面角的求法,考查几何法与向量法的应用,考查空间想象能力以及计算能力.

 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案| A. | 2 | B. | 1 | C. | $\frac{1}{2}$ | D. | $\frac{1}{4}$ |
| x | $\sqrt{2}$ | 2 | 4 |
| y | $\frac{\sqrt{2}}{2}$ | 0 | 4 |
(2)已知直线l:x=my+1与椭圆C2相交于不同两点M,N,且满足$\overrightarrow{OM}⊥\overrightarrow{ON}$,求参数m的值.
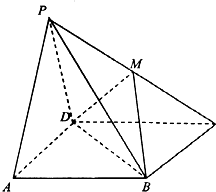 如图,四棱锥P-ABCD中,平面PAD⊥平面ABCD,PA=PD=4,底面ABCD是边长为4的正方形,若M为PC的中点.
如图,四棱锥P-ABCD中,平面PAD⊥平面ABCD,PA=PD=4,底面ABCD是边长为4的正方形,若M为PC的中点.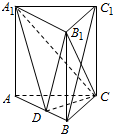 已知三棱柱ABC-A1B1C1中,侧棱垂直于底面,AC=BC,点D是AB的中点.求证:
已知三棱柱ABC-A1B1C1中,侧棱垂直于底面,AC=BC,点D是AB的中点.求证: