题目内容
6．设函数f（x）=$\left\{\begin{array}{l}{log_2}x，x＞0\\{4^x}，x≤0\end{array}$则f（f（$\frac{1}{2}$））=$\frac{1}{4}$；若函数g（x）=f（x）-k存在两个零点，则实数k的取值范围是（0.1]．分析 直接利用分段函数求解第一个空，利用函数的图象求解第二问．
解答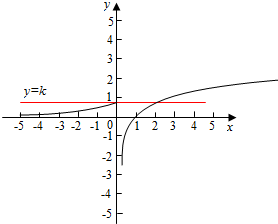 
解：函数f（x）=$\left\{\begin{array}{l}{log_2}x，x＞0\\{4^x}，x≤0\end{array}$则f（f（$\frac{1}{2}$））=f（-1）=$\frac{1}{4}$；
函数g（x）=f（x）-k存在两个零点，即f（x）=k存在两个解，如图：
可得a∈（0，1]．
故答案为：$\frac{1}{4}$；（0，1]．
点评 本题考查函数的零点以及分段函数的应用，考查数形结合以及计算能力．
练习册系列答案
相关题目
17．已知椭圆$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1（a＞b＞0）的左、右焦点分别为F1，F2，P是椭圆上一点，|PF1|=|F1F2|且cos∠PF2F1=$\frac{2}{3}$，则椭圆离心率为（ ）
| A． | $\frac{1}{2}$ | B． | $\frac{3}{7}$ | C． | $\frac{2}{3}$ | D． | $\frac{3}{4}$ |
已知椭圆$\frac{{x}^{2}}{{a}^{2}}+\frac{{y}^{2}}{{b}^{2}}$=1（a＞b＞0）的左焦点为F（-$\sqrt{3}$，0），过点F的直线交椭圆与A，B两点，当直线AB垂直x轴时，|AB|=$\frac{a}{2}$．
1．已知椭圆E：$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1（a＞b＞0）过点P（3，1），其左、右焦点分别为F1、F2，且$\overrightarrow{{F}_{1}P}$•$\overrightarrow{{F}_{2}P}$=-6，则椭圆E的离心率是（ ）
| A． | $\frac{\sqrt{2}}{3}$ | B． | $\frac{1}{2}$ | C． | $\frac{\sqrt{2}}{2}$ | D． | $\frac{2\sqrt{2}}{3}$ |
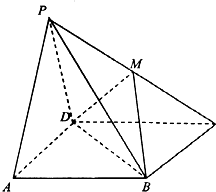如图，四棱锥P-ABCD中，平面PAD⊥平面ABCD，PA=PD=4，底面ABCD是边长为4的正方形，若M为PC的中点．