题目内容
15．已知函数f（x）=$\frac{1-{2}^{x}}{2+{2}^{x+1}}$，证明：函数f（x）为R上的减函数．分析 设x1＜x2，代入函数解析式化简f（x1）-f（x2），根据指数函数的单调性判断出符号，由函数单调性的定义即可得到结论．
解答 证明：解：设x1＜x2，则f（x1）-f（x2）=$\frac{1-{2}^{{x}_{1}}}{2+{2}^{{x}_{1}+1}}$-$\frac{1-{2}^{{x}_{2}}}{2+{2}^{{x}_{2}+1}}$
=$\frac{（1-{2}^{{x}_{1}}）（1+{2}^{{x}_{2}}）-（1-{2}^{{x}_{2}}）（1+{2}^{{x}_{1}}）}{2（1+{2}^{{x}_{1}}）（1+{2}^{{x}_{2}}）}$
=$\frac{{2}^{{x}_{2}}-{2}^{{x}_{1}}}{（1+{2}^{{x}_{1}}）（1+{2}^{{x}_{2}}）}$，
∵x1＜x2，∴${2}^{{x}_{2}}＞{2}^{{x}_{1}}$，则$\frac{{2}^{{x}_{2}}-{2}^{{x}_{1}}}{（1+{2}^{{x}_{1}}）（1+{2}^{{x}_{2}}）}＞0$，
∴f（x1）-f（x2）＞0，有f（x1）＞f（x2），
∴f（x）在（-∞，+∞）上为减函数．
点评 本题考查函数的单调性的证明，即设值、作差、变形、定号、下结论，考查化简、变形能力，属于中档题．
练习册系列答案
相关题目
10．不等式x2+ax+b＜0的解集是（-1，3），则（ ）
| A． | $\left\{\begin{array}{l}{a=2}\\{b=3}\end{array}\right.$ | B． | $\left\{\begin{array}{l}{a=-2}\\{b=-3}\end{array}\right.$ | C． | $\left\{\begin{array}{l}{a=1}\\{b=-6}\end{array}\right.$ | D． | $\left\{\begin{array}{l}{a=3}\\{b=2}\end{array}\right.$ |
20．设A，B是平面内的两个定点，且|AB|=2c＞0，该平面内动点P满足$\overrightarrow{PA}$•$\overrightarrow{PB}$=-k2（k＞0），请讨论动点P的轨迹．
4．在△ABC中，若sin2A+sin2B=5sin2C，当∠C取得最大值时，则sin2C=（ ）
| A． | $\frac{24}{25}$ | B． | $\frac{12}{25}$ | C． | $\frac{7}{16}$ | D． | $\frac{11}{16}$ |
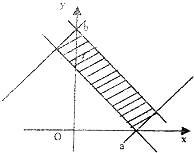设满足y≥|x-a|的点（x，y）的集合为A，满足y≤-|x|+b的点（x，y）的集合为B，其中a、b是正数，且A∩B≠∅．