题目内容
已知函数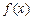 的导函数
的导函数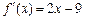 ,且
,且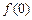 的值为整数,当
的值为整数,当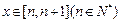 时,
时,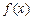 所有可能取的整数值有且只有1个,则
所有可能取的整数值有且只有1个,则 。
。
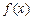 的导函数
的导函数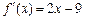 ,且
,且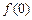 的值为整数,当
的值为整数,当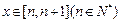 时,
时,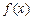 所有可能取的整数值有且只有1个,则
所有可能取的整数值有且只有1个,则 。
。4
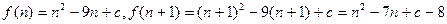 ,由题意得
,由题意得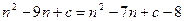 ,所以n
,所以n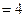 。
。
练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
题目内容
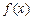 的导函数
的导函数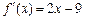 ,且
,且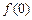 的值为整数,当
的值为整数,当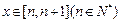 时,
时,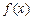 所有可能取的整数值有且只有1个,则
所有可能取的整数值有且只有1个,则 。
。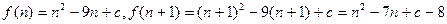 ,由题意得
,由题意得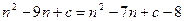 ,所以n
,所以n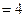 。
。
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案