题目内容
设函数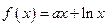 ,
,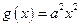 .
.
⑴当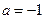 时,求函数
时,求函数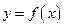 图象上的点到直线
图象上的点到直线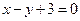 距离的最小值;
距离的最小值;
⑵是否存在正实数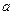 ,使
,使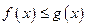 对一切正实数
对一切正实数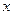 都成立?若存在,求出
都成立?若存在,求出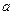 的取值范围;若不存在,请说明理由.
的取值范围;若不存在,请说明理由.
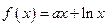 ,
,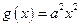 .
.⑴当
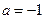 时,求函数
时,求函数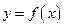 图象上的点到直线
图象上的点到直线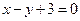 距离的最小值;
距离的最小值;⑵是否存在正实数
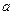 ,使
,使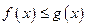 对一切正实数
对一切正实数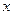 都成立?若存在,求出
都成立?若存在,求出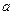 的取值范围;若不存在,请说明理由.
的取值范围;若不存在,请说明理由. (1)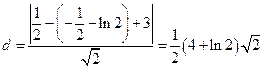 ;
;
(2)存在正数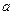 ,
,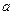 的取值范围为
的取值范围为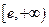
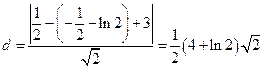 ;
;(2)存在正数
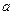 ,
,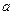 的取值范围为
的取值范围为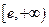
⑴由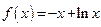 得
得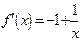 ,令
,令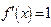 得
得 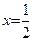
∴所求距离的最小值即为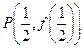 到直线
到直线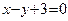 的距离
的距离
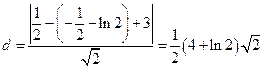
⑵假设存在正数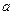 ,令
,令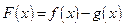
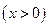 则
则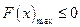
由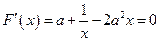 得:
得: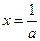
∵当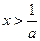 时,
时,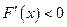 ,∴
,∴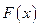 为减函数;
为减函数;
当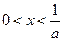 时,
时,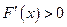 ,∴
,∴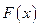 为增函数.
为增函数.
∴
∴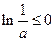 ∴
∴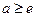
∴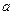 的取值范围为
的取值范围为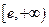
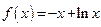 得
得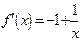 ,令
,令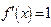 得
得 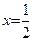
∴所求距离的最小值即为
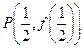 到直线
到直线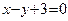 的距离
的距离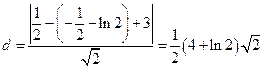
⑵假设存在正数
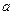 ,令
,令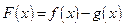
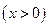 则
则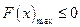
由
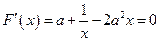 得:
得: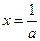
∵当
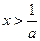 时,
时,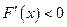 ,∴
,∴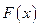 为减函数;
为减函数;当
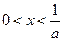 时,
时,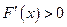 ,∴
,∴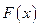 为增函数.
为增函数.∴

∴
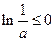 ∴
∴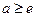
∴
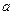 的取值范围为
的取值范围为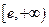

练习册系列答案
相关题目
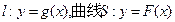 . 若直线l与曲线S同时满足下列两个条件:
. 若直线l与曲线S同时满足下列两个条件: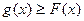 . 则称直线l为曲线S的“上夹线”.
. 则称直线l为曲线S的“上夹线”.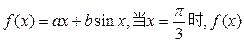 取得极小值
取得极小值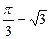 ,求a,b的值;
,求a,b的值;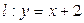 是(2)中曲线
是(2)中曲线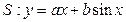 的“上夹线”。
的“上夹线”。 x3 +
x3 +  ax2 + 2ax (x∈R). (Ⅰ)当a = 1时,求函数f (x)的单调递增区间; (Ⅱ)函数f (x) 能否在R上单调递减,若是,求出a的取值范围;若不能,请说明理由; (Ⅲ)若函数f (x)在[-1,1]上单调递增,求a的取值范围.
ax2 + 2ax (x∈R). (Ⅰ)当a = 1时,求函数f (x)的单调递增区间; (Ⅱ)函数f (x) 能否在R上单调递减,若是,求出a的取值范围;若不能,请说明理由; (Ⅲ)若函数f (x)在[-1,1]上单调递增,求a的取值范围.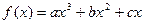 (
(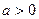 )的图象关于原点对称,
)的图象关于原点对称,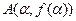 、
、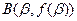 分别为函数
分别为函数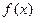 的极大值点和极小值点,且|AB|=2,
的极大值点和极小值点,且|AB|=2, .
.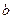 的值;
的值; 恒成立,求实数
恒成立,求实数 的取值范围.
的取值范围.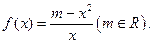
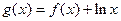 ,当m≥
,当m≥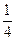 时,求g(x)在[
时,求g(x)在[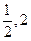 ]上的最大值;
]上的最大值;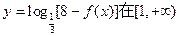 上是单调减函数,求实数m的取值范围.
上是单调减函数,求实数m的取值范围.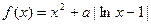 .(Ⅰ)当
.(Ⅰ)当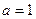 时,求曲线
时,求曲线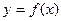 在
在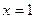 处的切线方程; (Ⅱ)当
处的切线方程; (Ⅱ)当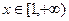 时,求函数
时,求函数 的最小值.
的最小值.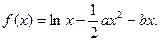 (1)当
(1)当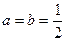 时,求
时,求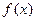 的最大值;(2)令
的最大值;(2)令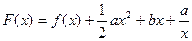 ,(0
,(0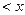 ≤3),其图象上任意一点
≤3),其图象上任意一点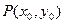 处切线的斜率
处切线的斜率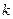 ≤
≤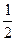 恒成立,求实数
恒成立,求实数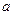 的取值范围;(3)当
的取值范围;(3)当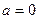 ,
,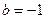 ,方程
,方程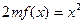 有唯一实数解,求正数
有唯一实数解,求正数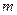 的值。
的值。 ,
, ,其中
,其中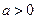 . 设两曲线
. 设两曲线 ,
, 有公共点,且在该点处的切线相同.(I)用
有公共点,且在该点处的切线相同.(I)用 表示
表示 ;(II)求证:
;(II)求证: (
( ).
).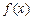 的导函数
的导函数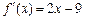 ,且
,且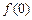 的值为整数,当
的值为整数,当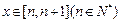 时,
时, 。
。