题目内容
设函数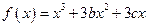 在两个极值点
在两个极值点 ,且
,且 。
。
(Ⅰ)求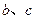 满足的约束条件,并在下面的坐标平面内,画出满足这些条件的点
满足的约束条件,并在下面的坐标平面内,画出满足这些条件的点 的区域;
的区域;

(II)证明:
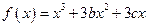 在两个极值点
在两个极值点 ,且
,且 。
。(Ⅰ)求
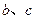 满足的约束条件,并在下面的坐标平面内,画出满足这些条件的点
满足的约束条件,并在下面的坐标平面内,画出满足这些条件的点 的区域;
的区域;
(II)证明:

(Ⅰ)
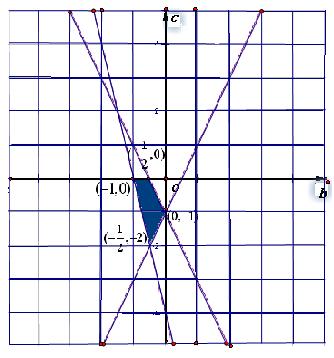
(II)证明见解析。
分析(I)这一问主要考查了二次函数根的分布及线性规划作可行域的能力。大部分考生有思路并能够得分。
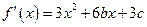 由题意知方程
由题意知方程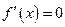 有两个根
有两个根

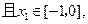
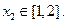 则有
则有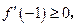
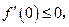
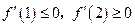 故有
故有
下图中阴影部分即是满足这些条件的点
 的区域。
的区域。
(II)这一问考生不易得分,有一定的区分度。主要原因是含字母较多,不易找到突破口。此题主要利用消元的手段,消去目标
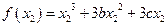 中的
中的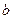 ,(如果消
,(如果消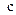 会较繁琐)再利用
会较繁琐)再利用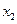 的范围,并借助(I)中的约束条件得
的范围,并借助(I)中的约束条件得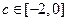 进而求解,有较强的技巧性。
进而求解,有较强的技巧性。由题意有
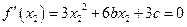 ............①
............①又
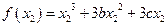 .....................②
.....................②消去
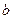 可得
可得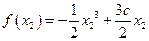 .
.又
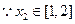 ,且
,且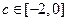
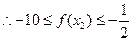

练习册系列答案
 阳光考场单元测试卷系列答案
阳光考场单元测试卷系列答案 名校联盟冲刺卷系列答案
名校联盟冲刺卷系列答案 名校提分一卷通系列答案
名校提分一卷通系列答案
相关题目
 ,其中
,其中 为常数.
为常数. 时,判断函数
时,判断函数 在定义域上的单调性;
在定义域上的单调性; ,不等式
,不等式 都成立.
都成立. .
. .试证明
.试证明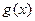 在区间
在区间  内是增函数;
内是增函数;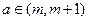 使得
使得 成立,求正整数
成立,求正整数 的值;
的值; 时,
时, 恒成立,求正整数
恒成立,求正整数 的最大值.
的最大值.

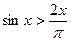


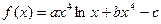 (x>0)在x = 1处
(x>0)在x = 1处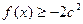 恒成立,求c的取值范围。(3分)
恒成立,求c的取值范围。(3分) 在
在 上是增函数,求
上是增函数,求 得取值范围;
得取值范围; ,
, ,求函数
,求函数 的最小值.
的最小值. ; 2.
; 2.
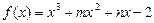 的图象过点(—1,—6),且函数
的图象过点(—1,—6),且函数 的图象关于y轴对称。 (1)求m、n的值及函数y=f(x)的单调区间;(2)若a>0,求函数y=f(x)在区间(a-1,a+1)内的极值.
的图象关于y轴对称。 (1)求m、n的值及函数y=f(x)的单调区间;(2)若a>0,求函数y=f(x)在区间(a-1,a+1)内的极值. 

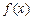 的导函数
的导函数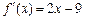 ,且
,且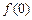 的值为整数,当
的值为整数,当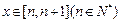 时,
时, 。
。