题目内容
(本小题满分12分)
已知函数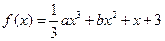 ,其中
,其中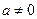 。
。
(1)当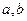 满足什么条件时,
满足什么条件时,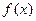 取得极值?
取得极值?
(2)已知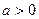 ,且
,且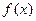 在区间
在区间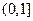 上单调递增,试用
上单调递增,试用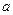 表示出
表示出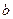 的取值范围。
的取值范围。
已知函数
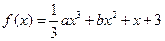 ,其中
,其中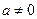 。
。(1)当
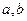 满足什么条件时,
满足什么条件时,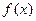 取得极值?
取得极值?(2)已知
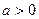 ,且
,且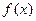 在区间
在区间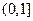 上单调递增,试用
上单调递增,试用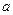 表示出
表示出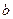 的取值范围。
的取值范围。(1)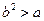
(2)当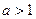 时,
时,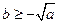 ;当
;当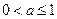 时,
时,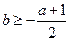 。
。
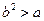
(2)当
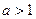 时,
时,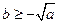 ;当
;当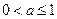 时,
时,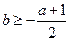 。
。(1)由已知得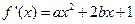 ,令
,令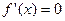 ,得
,得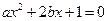 ,
,
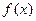 要取得极值,方程
要取得极值,方程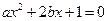 必须有解,
必须有解,
所以△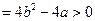 ,即
,即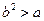 ,此时方程
,此时方程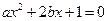 的根为
的根为
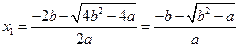 ,
,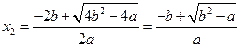 ,
,
所以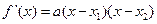 。
。
当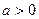 时,
时,
所以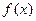 在x 1, x2处分别取得极大值和极小值;
在x 1, x2处分别取得极大值和极小值;
当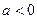 时,
时, 

所以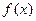 在x 1, x2处分别取得极大值和极小值。
在x 1, x2处分别取得极大值和极小值。
综上,当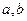 满足
满足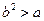 时,
时,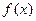 取得极值。
取得极值。
(2)要使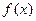 在区间
在区间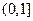 上单调递增,需使
上单调递增,需使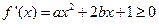 在
在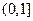 上恒成立。
上恒成立。
即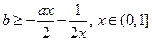 恒成立,所以
恒成立,所以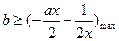
设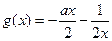 ,
,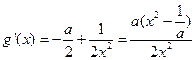 ,
,
令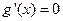 得
得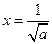 或
或 (舍去),
(舍去),
当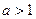 时,
时, ,当
,当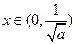 时
时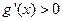 ,
,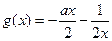 单调增函数;
单调增函数;
当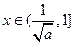 时
时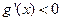 ,
,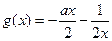 单调减函数,
单调减函数,
所以当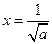 时,
时,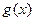 取得最大,最大值为
取得最大,最大值为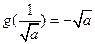 。
。
所以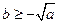
当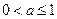 时,
时,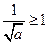 ,此时
,此时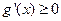 在区间
在区间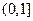 恒成立,所以
恒成立,所以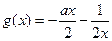 在区间
在区间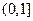 上单调递增,当
上单调递增,当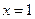 时
时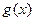 最大,最大值为
最大,最大值为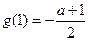 ,所以
,所以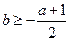
综上,当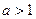 时,
时,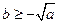 ;当
;当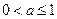 时,
时,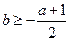 。
。
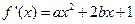 ,令
,令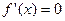 ,得
,得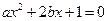 ,
,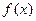 要取得极值,方程
要取得极值,方程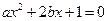 必须有解,
必须有解,所以△
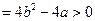 ,即
,即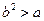 ,此时方程
,此时方程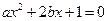 的根为
的根为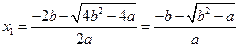 ,
,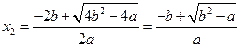 ,
,所以
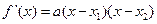 。
。当
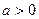 时,
时,| x | (-∞,x1) | x 1 | (x1,x2) | x2 | (x2,+∞) |
| f’(x) | + | 0 | - | 0 | + |
| f (x) | 增函数 | 极大值 | 减函数 | 极小值 | 增函数 |
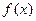 在x 1, x2处分别取得极大值和极小值;
在x 1, x2处分别取得极大值和极小值;当
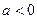 时,
时, 

| x | (-∞,x2) | x 2 | (x2,x1) | x1 | (x1,+∞) |
| f’(x) | - | 0 | + | 0 | - |
| f (x) | 减函数 | 极小值 | 增函数 | 极大值 | 减函数 |
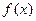 在x 1, x2处分别取得极大值和极小值。
在x 1, x2处分别取得极大值和极小值。综上,当
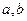 满足
满足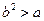 时,
时,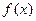 取得极值。
取得极值。(2)要使
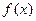 在区间
在区间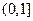 上单调递增,需使
上单调递增,需使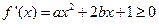 在
在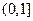 上恒成立。
上恒成立。即
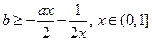 恒成立,所以
恒成立,所以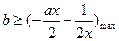
设
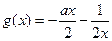 ,
,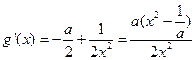 ,
,令
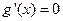 得
得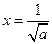 或
或 (舍去),
(舍去),当
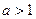 时,
时, ,当
,当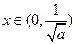 时
时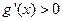 ,
,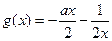 单调增函数;
单调增函数;当
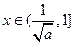 时
时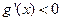 ,
,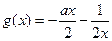 单调减函数,
单调减函数,所以当
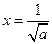 时,
时,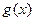 取得最大,最大值为
取得最大,最大值为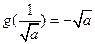 。
。所以
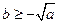
当
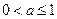 时,
时,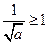 ,此时
,此时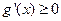 在区间
在区间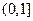 恒成立,所以
恒成立,所以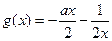 在区间
在区间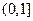 上单调递增,当
上单调递增,当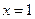 时
时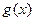 最大,最大值为
最大,最大值为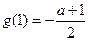 ,所以
,所以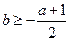
综上,当
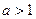 时,
时,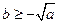 ;当
;当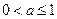 时,
时,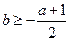 。
。
练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
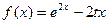 ,
,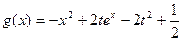 .
.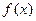 在区间
在区间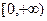 的最小值;(2)求证:若
的最小值;(2)求证:若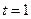 ,则不等式
,则不等式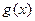 ≥
≥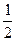 对于任意的
对于任意的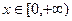 恒成立;(3)求证:若
恒成立;(3)求证:若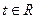 ,则不等式
,则不等式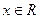 恒成立.
恒成立.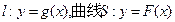 . 若直线l与曲线S同时满足下列两个条件:
. 若直线l与曲线S同时满足下列两个条件: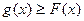 . 则称直线l为曲线S的“上夹线”.
. 则称直线l为曲线S的“上夹线”.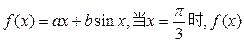 取得极小值
取得极小值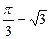 ,求a,b的值;
,求a,b的值;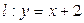 是(2)中曲线
是(2)中曲线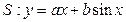 的“上夹线”。
的“上夹线”。
 有极值,求b的取值范围;
有极值,求b的取值范围; 处取得极值时,当
处取得极值时,当 恒成立,求c的取值范围;
恒成立,求c的取值范围; 都有
都有 .
.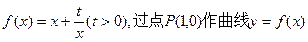 的两条切线PM、PN,切点分别为M、N.
的两条切线PM、PN,切点分别为M、N.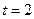 时,求函数
时,求函数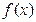 的单调递增区间;
的单调递增区间;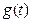 ,试求函数
,试求函数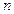 ,在区间
,在区间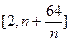 内,总存在m+1个数
内,总存在m+1个数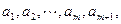 使得不等式
使得不等式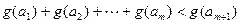 成立,求m的最大值.
成立,求m的最大值.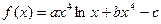 (x>0)在x = 1处
(x>0)在x = 1处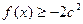 恒成立,求c的取值范围。(3分)
恒成立,求c的取值范围。(3分)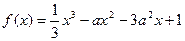 (a>0)
(a>0)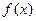 的单调区间,极大值,极小值
的单调区间,极大值,极小值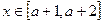 时,恒有
时,恒有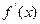 >
>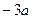 ,求实数a的取值范围
,求实数a的取值范围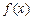 的导函数
的导函数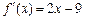 ,且
,且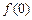 的值为整数,当
的值为整数,当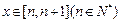 时,
时, 。
。