题目内容
数列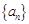 的各项都是正数,前
的各项都是正数,前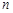 项和为
项和为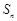 ,且对任意
,且对任意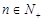 ,都有
,都有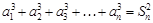 .
.
(1)求证: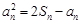 ; (2)求数列
; (2)求数列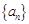 的通项公式。
的通项公式。
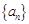 的各项都是正数,前
的各项都是正数,前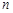 项和为
项和为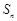 ,且对任意
,且对任意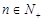 ,都有
,都有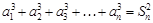 .
.(1)求证:
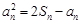 ; (2)求数列
; (2)求数列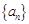 的通项公式。
的通项公式。(1)当 时,
时,
 ;
;
当 时,
时,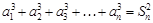 ①
①  ②两式相减。
②两式相减。
(2) 。
。
 时,
时,
 ;
;当
 时,
时,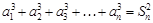 ①
①  ②两式相减。
②两式相减。(2)
 。
。试题分析:(1)当
 时,
时, 因为
因为 ,所以
,所以 1分
1分当
 时,
时,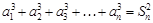 ①
①  ②
②①-②得,
 3分
3分因为
 所以
所以 ,
,即
 因为
因为 适合上式 所以
适合上式 所以
 6分
6分(2)由(I)知

 ③ 当
③ 当 时,
时,  ④
④③-④得
 -
- , 8分
, 8分因为
 ,所以
,所以 10分
10分所以数列
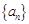 是等差数列,首项为1,公差为1,可得
是等差数列,首项为1,公差为1,可得 12分
12分点评:中档题,本题重点考查数列中
 的关系。研究方法是:讨论n=1的情况,当
的关系。研究方法是:讨论n=1的情况,当 时 ,一个研究两式的和差等,发现关系,即常说的“两步一验”,验证n=1时,适合与否,易于忽视。
时 ,一个研究两式的和差等,发现关系,即常说的“两步一验”,验证n=1时,适合与否,易于忽视。
练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
 中,
中, 
 则
则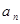 = .
= . 中,若
中,若 ,则
,则 ”为真命题,由于印刷问题,括号处的数模糊不清,可算得括号内的数为 .
”为真命题,由于印刷问题,括号处的数模糊不清,可算得括号内的数为 . 满足
满足 ,
, ,则
,则 。
。 的前13项和
的前13项和 ,则
,则 =( )
=( ) 中,
中, ,公差
,公差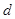 为整数,若
为整数,若 ,
, .
. 项和
项和 的最大值;
的最大值;  项的和
项的和 等于
等于



 首项为1,且
首项为1,且 成等比数列,
成等比数列,
 通项公式;
通项公式; 前n项和
前n项和 ;
; 成立,求
成立,求 范围.
范围.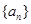 的首项
的首项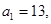 公差
公差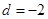 ,则当n=_________时,前n项和
,则当n=_________时,前n项和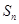 取得最大值.
取得最大值.