题目内容
等差数列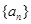 中,
中, 
 则
则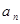 = .
= .
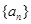 中,
中, 
 则
则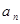 = .
= .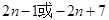
试题分析:根据题意,由于等差数列
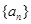 中,
中, 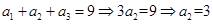
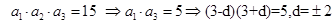 ,故可知首项有1,或者5,则可知其通项公式为
,故可知首项有1,或者5,则可知其通项公式为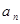 =
=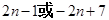
点评:主要是考查了等差数列的通项公式的求解,属于基础题。

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
题目内容
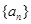 中,
中, 
 则
则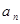 = .
= .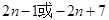
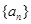 中,
中, 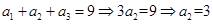
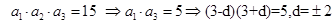 ,故可知首项有1,或者5,则可知其通项公式为
,故可知首项有1,或者5,则可知其通项公式为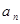 =
=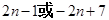

 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案