题目内容
若a>0,b>0,且函数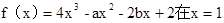 处有极值,则ab的最大值是 .
处有极值,则ab的最大值是 .
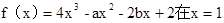 处有极值,则ab的最大值是 .
处有极值,则ab的最大值是 .9
试题分析:∵f′(x)=12x2-2ax-2b,又因为在x=1处有极值,故有f’(1)=0,∴a+b=6,∵a>0,b>0,∴ab≤(
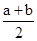 )2=9,当且仅当a=b=3时取等号,所以ab的最大值等于9,故答案为9.
)2=9,当且仅当a=b=3时取等号,所以ab的最大值等于9,故答案为9.点评:解决该试题的关键是函数在极值点处的导数值为0、考查利用基本不等式求最值需注意:一正、二定、三相等.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
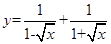
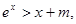 恒成立,则m的取值范围是 。
恒成立,则m的取值范围是 。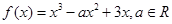
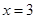 是
是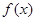 的极值点,求
的极值点,求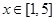 上的最大值
上的最大值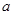 的取值范围.
的取值范围.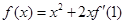 ,
,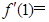 .
.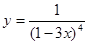 的导数.
的导数.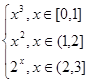 在区间[0,3]上的积分.
在区间[0,3]上的积分.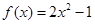 的图像上一点
的图像上一点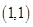 及邻近一点
及邻近一点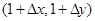 ,则
,则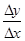 和
和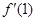 分别等于( )
分别等于( )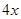 ,4
,4 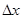 ,4
,4 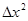 ,3
,3 的切线
的切线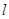 过点
过点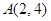 ,则切线
,则切线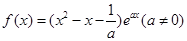 .
.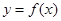 在点
在点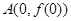 处的切线方程;
处的切线方程;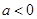 时,求函数
时,求函数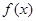 的单调区间.
的单调区间.