题目内容
(本小题满分12分)
已知函数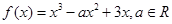
(1)若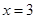 是
是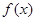 的极值点,求
的极值点,求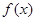 在
在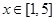 上的最大值
上的最大值
(2)若函数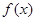 是R上的单调递增函数,求实数的
是R上的单调递增函数,求实数的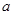 的取值范围.
的取值范围.
已知函数
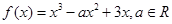
(1)若
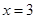 是
是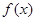 的极值点,求
的极值点,求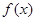 在
在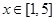 上的最大值
上的最大值(2)若函数
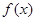 是R上的单调递增函数,求实数的
是R上的单调递增函数,求实数的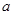 的取值范围.
的取值范围.(1)当 时,函数
时,函数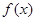 有最大值为15. (2)
有最大值为15. (2) 。
。
 时,函数
时,函数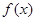 有最大值为15. (2)
有最大值为15. (2) 。
。试题分析:(1)根据
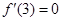 可求出a的值,从而再求出极值,与区间的端点值比较可求出最大值.
可求出a的值,从而再求出极值,与区间的端点值比较可求出最大值.(2) 函数
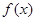 是R上的单调递增函数可转化为
是R上的单调递增函数可转化为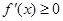 在R上恒成立问题来解决.
在R上恒成立问题来解决.(1)解:
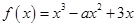 ,
,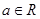 ,且当
,且当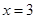 时有极值.
时有极值.可得:
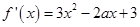 ---------------------- 1分
---------------------- 1分因为
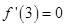 所以
所以 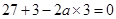
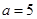 -------- 2分
-------- 2分则
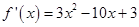 ------------------------- 3分
------------------------- 3分当
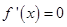 时,
时,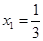 ,
,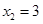
如表所示:
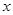 | 1 | 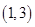 | 3 | 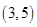 | 5 |
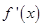 | | — | 0 | + | |
 | -1 | 单调递减 | 极小值 | 单调递增 | 15 |
当
 时,函数
时,函数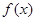 有最大值为15. ------------------------------ 6分
有最大值为15. ------------------------------ 6分(2)解:
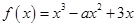 为在
为在 上的单调递增函数
上的单调递增函数则
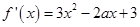 所以
所以 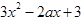 ≥0在R上恒成立,
≥0在R上恒成立,因此
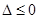 ------------------------- 8分
------------------------- 8分即
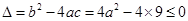 ---------
---------实数的
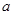 的取值范围是
的取值范围是  ------------------ 12 分
------------------ 12 分点评:连续函数在闭区间上最值不在极值处取得就是区间端点处取得.函数f(x)在R上单调递增,实质是
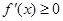 在R上恒成立.
在R上恒成立.
练习册系列答案
 星级口算天天练系列答案
星级口算天天练系列答案 芒果教辅达标测试卷系列答案
芒果教辅达标测试卷系列答案
相关题目
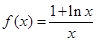

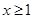 时,不等式
时,不等式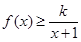 恒成立,求实数k的取值范围;
恒成立,求实数k的取值范围;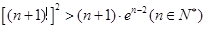 .
. .
.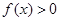 的解集为
的解集为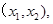 且方程
且方程 的两实根为
的两实根为 .
. ,求
,求 的关系式;
的关系式;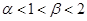 ,求证:
,求证: .
.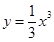 上的点
上的点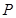 的切线
的切线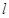 的方程为
的方程为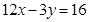 ,那么
,那么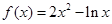 在其定义域的一个子区间
在其定义域的一个子区间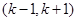 内部是单调函数,则实数
内部是单调函数,则实数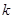 的取值范围是 ( )
的取值范围是 ( )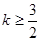
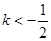
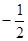 <
<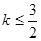
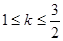
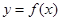 的图象在点
的图象在点 处的切线方程是
处的切线方程是 ,则
,则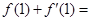 _.
_.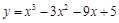 在区间
在区间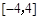 上的最大值为( ).
上的最大值为( ).
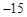
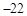
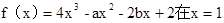 处有极值,则ab的最大值是 .
处有极值,则ab的最大值是 .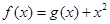 ,曲线
,曲线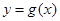 在点
在点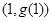 处的切线方程为
处的切线方程为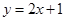 ,则曲线
,则曲线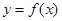 在点
在点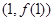 处切线的斜率为
处切线的斜率为