题目内容
已知△ABC中，BC=4，2sinC=2sinB+sinA.求顶点A的轨迹方程.
顶点A的轨迹方程是x2-
=1(x＞1).
=1(x＞1).如图所示,
以直线BC为x轴，线段BC的中垂线为y轴建立直角坐标系.
∵|BC|=4，∴B（-2，0），C（2，0），
由2sinC=2sinB+sinA，利用正弦定理可得
2|AB|=2|AC|+|BC|，
即|AB|-|AC|=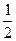
|BC|=2＜4，
即点A到点B的距离与到点C的距离之差是常数2.
由双曲线的定义可知，点A的轨迹是以B、C为焦点的双曲线的右支（除顶点）.
其中，2a=2,∴a=1.2c=4.∴c=2.从而b2=c2-a2=3.
∴顶点A的轨迹方程是x2-=1(x＞1).
以直线BC为x轴，线段BC的中垂线为y轴建立直角坐标系.
∵|BC|=4，∴B（-2，0），C（2，0），
由2sinC=2sinB+sinA，利用正弦定理可得
2|AB|=2|AC|+|BC|，
即|AB|-|AC|=
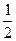|BC|=2＜4，即点A到点B的距离与到点C的距离之差是常数2.
由双曲线的定义可知，点A的轨迹是以B、C为焦点的双曲线的右支（除顶点）.
其中，2a=2,∴a=1.2c=4.∴c=2.从而b2=c2-a2=3.
∴顶点A的轨迹方程是x2-
=1(x＞1).
练习册系列答案
中考利剑中考试卷汇编系列答案
教育世家状元卷系列答案
相关题目
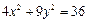有相同的焦点．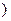
+
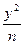=1(m>n>0)和双曲线
-
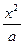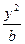=1(a>0,b>0)有相同的焦点F1、F2,P是这两条曲线的一个交点,则|PF1|·|PF2|等于( )
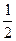(m-a)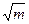
-
-
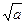
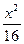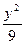=1上的一点P到点（5，0）的距离为15，则点P到点（-5，0）的距离是( )
-
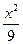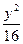=1上的一点P到双曲线的一个焦点的距离为3，则点P到另一个焦点的距离为__________.
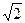,则双曲线方程为_____________.
