题目内容
如图所示,在△ABC中,点M是BC的中点,点N在边AC上,且AN=2NC,AM与BN相交于点P,求AP∶PM的值.


4
设 =e1,
=e1, =e2,
=e2,
则 =
= +
+ =-3e2-e1,
=-3e2-e1, =2e1+e2.
=2e1+e2.
∵A,P,M和B,P,N分别共线,∴存在λ,μ∈R,
使 =λ
=λ =-λe1-3λe2,
=-λe1-3λe2, =μ
=μ =2μe1+μe2.
=2μe1+μe2.
故 =
= -
- =(λ+2μ)e1+(3λ+μ)e2,
=(λ+2μ)e1+(3λ+μ)e2,
而 =
= +
+ =2e1+3e2,
=2e1+3e2,
∴ ∴
∴
∴ =
= ,∴
,∴ =
= ,即AP∶PM=4.
,即AP∶PM=4.
 =e1,
=e1, =e2,
=e2,则
 =
= +
+ =-3e2-e1,
=-3e2-e1, =2e1+e2.
=2e1+e2.∵A,P,M和B,P,N分别共线,∴存在λ,μ∈R,
使
 =λ
=λ =-λe1-3λe2,
=-λe1-3λe2, =μ
=μ =2μe1+μe2.
=2μe1+μe2.故
 =
= -
- =(λ+2μ)e1+(3λ+μ)e2,
=(λ+2μ)e1+(3λ+μ)e2,而
 =
= +
+ =2e1+3e2,
=2e1+3e2,∴
 ∴
∴
∴
 =
= ,∴
,∴ =
= ,即AP∶PM=4.
,即AP∶PM=4.
练习册系列答案
相关题目
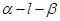 大小为
大小为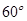 ,半平面
,半平面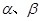 内分别有点A、B,
内分别有点A、B,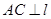 于C、
于C、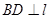 于D,已知AC=4、CD=5,DB=6,求线段AB的长.
于D,已知AC=4、CD=5,DB=6,求线段AB的长. ,求当|m|取最小值时实数t的值;
,求当|m|取最小值时实数t的值; ,若存在,请求出t;若不存在,请说明理由.
,若存在,请求出t;若不存在,请说明理由. ·
· =0,
=0, ·
·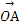 ,
,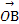 ,
,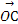 ,其中
,其中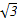 ,若
,若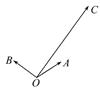


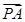 +3
+3 |的最小值为______.
|的最小值为______. =a,
=a, =b,
=b,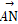 =3
=3 ,M是BC的中点,则
,M是BC的中点,则 = (用a,b表示).
= (用a,b表示). 