题目内容
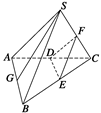
如图所示,正方体ABCD—A1B1C1D1中,侧面对角线AB1,BC1上分别有两点E,F,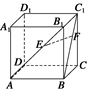 且B1E=C1F.求证:EF∥平面ABCD.
且B1E=C1F.求证:EF∥平面ABCD.
 且B1E=C1F.求证:EF∥平面ABCD.
且B1E=C1F.求证:EF∥平面ABCD.证明略
方法一 分别过E,F作EM⊥AB于M,FN⊥BC于N,连接MN.
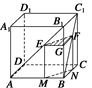
∵BB1⊥平面ABCD,
∴BB1⊥AB,BB1⊥BC,
∴EM∥BB1,FN∥BB1,
∴EM∥FN.
又∵B1E=C1F,∴EM=FN,
故四边形MNFE是平行四边形,∴EF∥MN.
又MN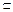 平面ABCD,EF
平面ABCD,EF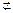 平面ABCD,
平面ABCD,
所以EF∥平面ABCD.
方法二 过E作EG∥AB交BB1于G,
连接GF,则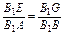 ,
,
∵B1E=C1F,B1A=C1B,
∴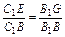 ,∴FG∥B1C1∥BC,
,∴FG∥B1C1∥BC,
又EG∩FG=G,AB∩BC=B,
∴平面EFG∥平面ABCD,而EF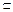 平面EFG,
平面EFG,
∴EF∥平面ABCD.

∵BB1⊥平面ABCD,
∴BB1⊥AB,BB1⊥BC,
∴EM∥BB1,FN∥BB1,
∴EM∥FN.
又∵B1E=C1F,∴EM=FN,
故四边形MNFE是平行四边形,∴EF∥MN.
又MN
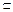 平面ABCD,EF
平面ABCD,EF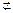 平面ABCD,
平面ABCD,所以EF∥平面ABCD.
方法二 过E作EG∥AB交BB1于G,
连接GF,则
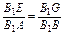 ,
,∵B1E=C1F,B1A=C1B,
∴
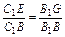 ,∴FG∥B1C1∥BC,
,∴FG∥B1C1∥BC,又EG∩FG=G,AB∩BC=B,
∴平面EFG∥平面ABCD,而EF
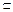 平面EFG,
平面EFG,∴EF∥平面ABCD.

练习册系列答案
 暑假作业暑假快乐练西安出版社系列答案
暑假作业暑假快乐练西安出版社系列答案
相关题目
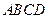 是平行四边形,点
是平行四边形,点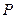 是平面
是平面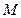 是
是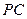 的中点,在
的中点,在 上取一点
上取一点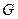 ,过
,过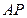 作平面交平面
作平面交平面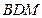 于
于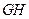 .
.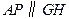 .
.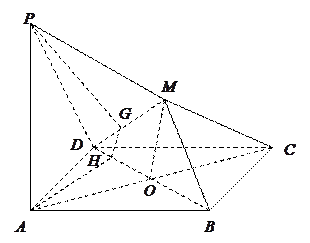
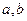 是两条异面直线,
是两条异面直线,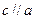 ,那么
,那么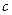 与
与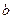 的位置关系____________________。
的位置关系____________________。