题目内容
1.已知复数z满足条件|z-3i|=1,则|z|最小值为2.分析 根据已知等式的几何意义以及|z|的几何意义求最值.
解答 解:设复数z=x+yi,则|z-3i|=1,为x2+(y-3)2=1,表示以(0,3)为圆心,1为半径的圆,所以|z|表示圆上的点到原点的距离,所以它的最小值为3-1=2;
故答案为:2.
点评 本题考查了复数模的几何意义的运用求最值;关键是明确已知|z-3i|=1表示圆.

练习册系列答案
相关题目
11.已知tan(π-x)=$\frac{3}{4}$,则tan2x等于( )
| A. | $\frac{7}{24}$ | B. | -$\frac{7}{24}$ | C. | $\frac{24}{7}$ | D. | -$\frac{24}{7}$ |
12.如图,一个子弹运动的轨迹是一个三次函数图象的一部分,则这个函数的解析式是( )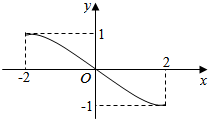

| A. | y=-$\frac{1}{3}$x3+$\frac{5}{6}$x | B. | y=$\frac{1}{3}$x3-$\frac{11}{6}x$ | C. | y=$\frac{2}{3}{x}^{3}$-$\frac{19}{6}x$ | D. | y=$\frac{1}{16}{x}^{3}-\frac{3}{4}x$ |
9.已知cosα=$\frac{5}{13}$,α是第一象限角,则sin(π+α)的值为( )
| A. | $\frac{5}{13}$ | B. | -$\frac{5}{13}$ | C. | $\frac{12}{13}$ | D. | -$\frac{12}{13}$ |
16.某中学调查了某班全部50名同学参加数学兴趣小组和物理兴趣小组的情况,数据如下表:(单位:人)
(Ⅰ)从该班随机选一名同学,求该同学至少参加上述一个兴趣小组的概率;
(Ⅱ)在既参加数学兴趣小组,又参加物理兴趣小组的7名同学中,有4名男同学A,B,C,D,3名女同学a,b,c,现从这4名男同学和3名女同学中各随机选1人,求A被选中且a未被选中的概率.
| 参加数学兴趣小组 | 不参加数学兴趣小组 | |
| 参加物理兴趣小组 | 7 | 10 |
| 不参加物理兴趣小组 | 7 | 26 |
(Ⅱ)在既参加数学兴趣小组,又参加物理兴趣小组的7名同学中,有4名男同学A,B,C,D,3名女同学a,b,c,现从这4名男同学和3名女同学中各随机选1人,求A被选中且a未被选中的概率.
13.已知i为虚数单位,则复数$\frac{1+2i}{2-i}$=( )
| A. | i | B. | -i | C. | -$\frac{4}{5}$-$\frac{3}{5}$i | D. | -$\frac{4}{5}$+$\frac{3}{5}$i |