题目内容
8.已知函数f(x)=lnx-ax2-bx.当a=-1时,若函数f(x)在其定义域内是增函数,求b的取值范围.分析 问题转化为$b≤\frac{1}{x}+2x$对x∈(0,+∞)恒成立,结合函数的单调性,求出$\frac{1}{x}$+2x的最小值即可.
解答 解:依题意:f(x)=lnx+x2-bx,
∵f(x)在(0,+∞)上递增,
∴$f'(x)=\frac{1}{x}+2x-b≥0$对x∈(0,+∞)恒成立,
即$b≤\frac{1}{x}+2x$对x∈(0,+∞)恒成立,
∴只需$b≤{(\frac{1}{x}+2x)_{min}}$,
∵x>0,∴$\frac{1}{x}+2x≥2\sqrt{2}$,
当且仅当$x=\frac{{\sqrt{2}}}{2}$时取“=”,
∴$b≤2\sqrt{2}$,
∴b的取值范围为:(-∞,2$\sqrt{2}$].
点评 本题考查了函数的单调性最值问题,考查函数恒成立问题,是一道中档题.

练习册系列答案
相关题目
13.已知集合A={x|(x+1)(4-x)<0},集合B={y|y=2sin3x},则A∩B=( )
| A. | (-1,2] | B. | ( 2,4 ) | C. | [-2,-1 ) | D. | [-2,2] |
20.函数$y=\sqrt{\frac{x-6}{x-1}}$的定义域为( )
| A. | (-∞,1]∪[6,+∞) | B. | (-∞,1)∪[6,+∞) | C. | (-3,1)∪(2,+∞) | D. | [-3,1)∪(2,+∞) |
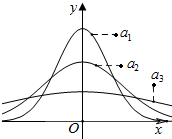 如图分别是正态分布N(0,σ12),N(0,σ22),N(0,σ32)在同一坐标平面的分布密度曲线,则σ1、σ2、σ3的大小关系为σ1<σ2<σ3.
如图分别是正态分布N(0,σ12),N(0,σ22),N(0,σ32)在同一坐标平面的分布密度曲线,则σ1、σ2、σ3的大小关系为σ1<σ2<σ3.