题目内容
【题目】已知抛物线
，过点
的直线
交抛物线于
、
两点，设
为坐标原点，点
.
（1）求
的值；
（2）若
，
，
的面积成等比数列，求直线的方程.
【答案】（1）
（2）直线
的方程为
或
【解析】
（1）根据直线
的倾斜角与角
的关系，即可用直线的斜率以及两角和与差的正切公式求出
的值.
（2）将条件“
的面积成等比数列”等价转化为“
成等比数列”，再将直线的方程代入抛物线方程，利用韦达定理得到
的值，结合条件即可建立关于直线的斜率
的方程，从而求出斜率，得到直线的方程.
解：（1）由题意直线
，
斜率均存在，且
，
.
∴
.
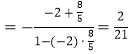故.
（2）由（1）知点
为抛物线的焦点
据题意，直线的斜率存在且不为0，故可设直线的方程为
.
由
.
设
、
，则有
，
，
.
若
，
，
的面积成等比数列，则
，
，
成等比数列
∴
，即：
.
∴
∴
，则
.
解得，
或
，均满足
.
故直线的方程为或.
100分闯关期末冲刺系列答案
名校联盟快乐课堂系列答案
【题目】现对某市工薪阶层关于“楼市限购令”的态度进行调查，随机抽调了50人，他们月收入的频数分布及对“楼市限购令”赞成人数如下表.
月收入(单位百元) |
|
|
|
|
|
|
频数 | 5 | 10 | 15 | 10 | 5 | 5 |
赞成人数 | 4 | 8 | 12 | 5 | 2 | 1 |
(1)由以上统计数据填下面2×2列联表，并问是否有99％的把握认为“月收入以5500元为分界点对“楼市限购令”的态度有差异；
月收入不低于55百元的人数 | 月收入低于55百元的人数 | 合计 | |
赞成 | a=______________ | c=______________ | ______________ |
不赞成 | b=______________ | d=______________ | ______________ |
合计 | ______________ | ______________ | ______________ |
(2)试求从年收入位于
（单位：百元）的区间段的被调查者中随机抽取2人，恰有1位是赞成者的概率。
参考公式：
，其中
.
参考值表：
| 0.50 | 0.40 | 0.25 | 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| 0.455 | 0.708 | 1.323 | 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
