题目内容
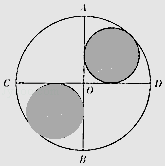
【题目】已知圆![]() ,圆心为
,圆心为![]() ,定点
,定点![]() ,P为圆
,P为圆![]() 上一点,线段
上一点,线段![]() 上一点N满足
上一点N满足![]() ,直线
,直线![]() 上一点Q,满足
上一点Q,满足![]() .
.
(Ⅰ) 求点Q的轨迹C的方程;
(Ⅱ) O为坐标原点, ![]() 是以
是以![]() 为直径的圆,直线
为直径的圆,直线![]() 与
与![]() 相切,并与轨迹C交于不同的两点A,B. 当
相切,并与轨迹C交于不同的两点A,B. 当![]() 且满足
且满足![]() 时,求△OAB面积S的取值范围.
时,求△OAB面积S的取值范围.
【答案】(Ⅰ)![]() .(Ⅱ)
.(Ⅱ)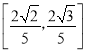 .
.
【解析】试题分析:(Ⅰ)直接根据已知条件结合椭圆的定义求出曲线的方程.
(Ⅱ)利用直线和曲线的位置关系建立方程组,进一步利用一元二次方程根和系数的关系建立关系式,进一步求出参数的取值范围.
试题解析:
(Ⅰ)∵![]()
∴ N为![]() 的中点
的中点
∵![]()
∴ QN为线段![]() 的中垂线
的中垂线
∴![]()
∵![]()
∴由椭圆的定义可知Q的轨迹是以![]() 为焦点,长轴长为
为焦点,长轴长为![]() 的椭圆,
的椭圆,
设椭圆的标准方程为![]() ,
,
则![]() ,
,
∴![]() .
.
∴点Q的轨迹C的方程为![]() .
.
(Ⅱ)∵圆O与直线![]() 相切,
相切,
∴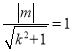 ,即
,即![]() ,
,
由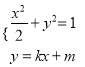 ,消去y整理得
,消去y整理得![]() .
.
∵直线![]() 与椭圆交于两个不同点,
与椭圆交于两个不同点,
∴![]() ,
,
将![]() 代入上式,可得
代入上式,可得![]() ,
,
设![]() ,
,
则![]() ,
,
∴![]() ,
,
∴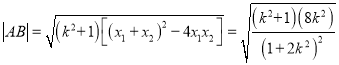 ,
,
∴![]() ,
,
∵![]() ,解得
,解得![]() .
.
满足![]() .
.
又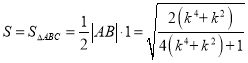 ,
,
设![]() ,则
,则![]() .
.
∴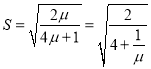 ,
,
∴![]()
故△OAB面积S的取值范围为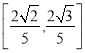 .
.

练习册系列答案
相关题目