题目内容
已知定义在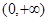 的函数
的函数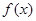 ,对任意的
,对任意的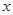 、
、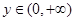 ,都有
,都有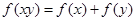 ,且当
,且当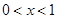 时,
时,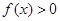 .
.
(1)证明:当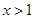 时,
时,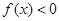 ;
;
(2)判断函数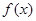 的单调性并加以证明;
的单调性并加以证明;
(3)如果对任意的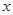 、
、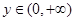 ,
,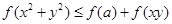 恒成立,求实数
恒成立,求实数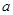 的取值范围.
的取值范围.
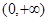 的函数
的函数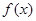 ,对任意的
,对任意的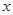 、
、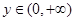 ,都有
,都有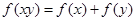 ,且当
,且当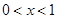 时,
时,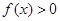 .
.(1)证明:当
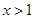 时,
时,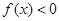 ;
;(2)判断函数
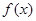 的单调性并加以证明;
的单调性并加以证明;(3)如果对任意的
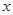 、
、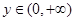 ,
,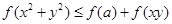 恒成立,求实数
恒成立,求实数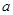 的取值范围.
的取值范围.(1)先证明 ,进而证明当
,进而证明当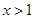 时,
时,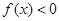 ;
;
(2)严格按照单调函数的定义证明即可;
(3)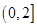
 ,进而证明当
,进而证明当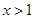 时,
时,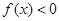 ;
;(2)严格按照单调函数的定义证明即可;
(3)
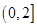
试题分析:(1)证明:取
 ,
,又
 ,即
,即 ,
,所以当
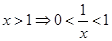 时,
时,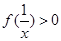 ;
; .
. (2)
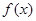 在
在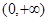 上是减函数,证明如下:
上是减函数,证明如下:设
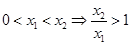 ,
,
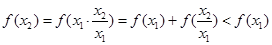
 在
在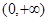 上是减函数.
上是减函数.(3)
 ,
,而
 ,所以实数
,所以实数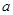 的取值范围为
的取值范围为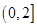 .
. 点评:解决抽象函数问题的主要方法是“赋值法”,而且抽象函数的单调性的证明知能用定义,利
用基本不等式求最值时,要注意“一正二定三相等”三个条件缺一不可.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目

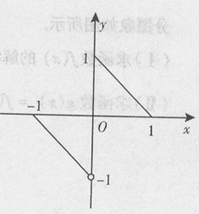
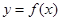 满足:
满足: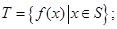 (ii)对任意
(ii)对任意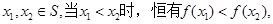
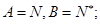
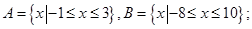
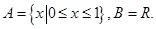
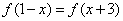 ,且
,且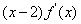 <0a="f" (
<0a="f" (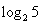 ),b="f" (
),b="f" (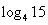 ),c="f" (
),c="f" (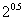 ),则a,b,c的大小关系为
),则a,b,c的大小关系为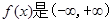 上的奇函数,且
上的奇函数,且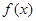 的图象关于直线x=1对称,当
的图象关于直线x=1对称,当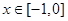 时,
时,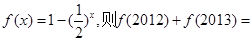 .
.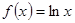 ,
,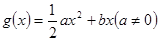
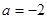 时,
时,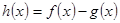 在其定义域内单调递增,求
在其定义域内单调递增,求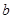 的取值范围;
的取值范围;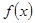 的图象
的图象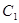 与函数
与函数 的图象
的图象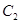 交于
交于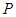 ,
,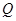 两点,过线段
两点,过线段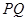 的中点
的中点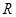 作
作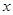 轴的垂线分别交
轴的垂线分别交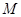 ,
,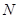 ,问是否存在点
,问是否存在点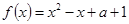
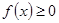 对一切实数x恒成立,求实数a的取值范围。
对一切实数x恒成立,求实数a的取值范围。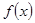 在区间
在区间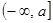 上的最小值
上的最小值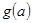 的表达式。
的表达式。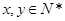 ,且
,且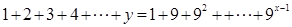 ,当
,当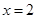 时,
时, 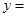 ;若把
;若把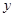 表示成
表示成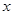 的函数,其解析式是
的函数,其解析式是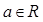 ,函数
,函数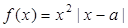 .
.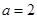 时,求使
时,求使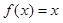 成立的
成立的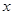 的集合;
的集合;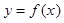 在区间
在区间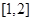 上的最小值.
上的最小值.