题目内容
函数y=f(x)的图象如图所示,则不等式f(x)<f(-x)+x的解集为______。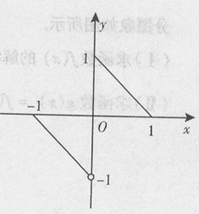

{x|-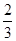 <x<0或
<x<0或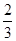 <x≤1}
<x≤1}
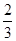 <x<0或
<x<0或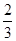 <x≤1}
<x≤1}试题分析:根据图像可知,函数的解析式,那么可以知道0<x<1,f(x)=-x+1,-1<x<0,f(x)=-x-1
那么可知不等式f(x)<f(-x)+x,需要对x分类讨论得到
当0<x<1,-1<-x<0则原式表示为(-x+1)<x-1+x,1>x>
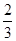
当-1<x<0原式等价于-x-1<x+1+x,解得-
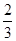 <x<0,当x=1时,则可知也成立,因此综上所知,不等式的解集为{x|-
<x<0,当x=1时,则可知也成立,因此综上所知,不等式的解集为{x|-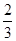 <x<0或
<x<0或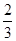 <x≤1},答案为{x|-
<x≤1},答案为{x|-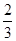 <x<0或
<x<0或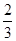 <x≤1}。
<x≤1}。点评:解决该试题的关键是根据图像分析函数的奇函数性质,然后化简不等式,结合特殊值的函数关系式来求解。

练习册系列答案
 全能练考卷系列答案
全能练考卷系列答案 一课一练课时达标系列答案
一课一练课时达标系列答案
相关题目
 .
.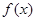 的单调性;
的单调性;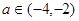 及
及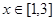 时,恒有
时,恒有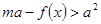 成立,求实数
成立,求实数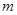 的取值范围.
的取值范围.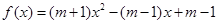
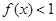 的解集为
的解集为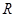 ,求
,求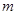 的取值范围;
的取值范围;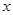 的不等式
的不等式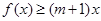 ;
;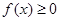 对一切
对一切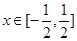 恒成立,求
恒成立,求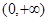 的函数
的函数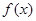 ,对任意的
,对任意的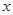 、
、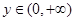 ,都有
,都有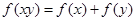 ,且当
,且当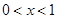 时,
时,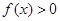 .
.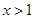 时,
时,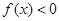 ;
;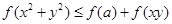 恒成立,求实数
恒成立,求实数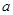 的取值范围.
的取值范围.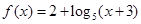 在区间[-2,2]上的值域是____________
在区间[-2,2]上的值域是____________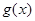 是
是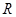 上的奇函数,且当
上的奇函数,且当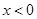 时
时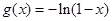 ,函数
,函数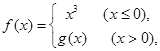 若
若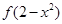 >
>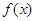 ,则实数
,则实数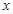 的取值范围是
的取值范围是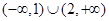
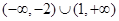

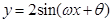 为偶函数(0<θ<π), 其图象与直线y=2的交点的横坐标为
为偶函数(0<θ<π), 其图象与直线y=2的交点的横坐标为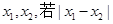 的最小值为π,则( )
的最小值为π,则( )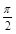
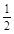 ,θ=
,θ=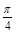
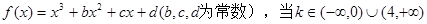 时,
时,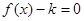 只有一个实根;当
只有一个实根;当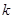 ∈(0,4)时,
∈(0,4)时,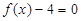 和
和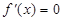 有一个相同的实根;
有一个相同的实根;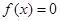 和
和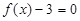 的任一实根大于
的任一实根大于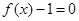 的任一实根;
的任一实根; 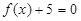 的任一实根小于
的任一实根小于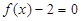 的任一实根.
的任一实根.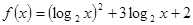 ,
,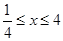 ,
,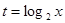 ,求
,求 取值范围;
取值范围; 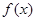 的最值,并给出函数取最值时对应的x的值。
的最值,并给出函数取最值时对应的x的值。