题目内容
已知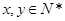 ,且
,且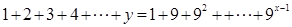 ,当
,当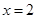 时,
时, 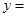 ;若把
;若把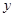 表示成
表示成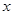 的函数,其解析式是
的函数,其解析式是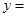 .
.
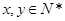 ,且
,且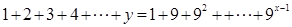 ,当
,当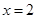 时,
时, 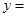 ;若把
;若把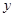 表示成
表示成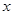 的函数,其解析式是
的函数,其解析式是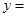 .
.4; 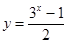
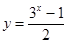
试题分析:由
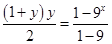 得:
得: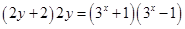
又
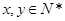 因此
因此 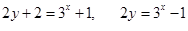
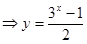 。
。点评:基础题,从给定等式不难想到,等式的左右两边,可分别应用等差数列、等比数列的求和公式化简后,进一步写出x,y关系。

练习册系列答案
相关题目
题目内容
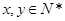 ,且
,且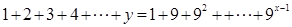 ,当
,当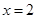 时,
时, 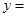 ;若把
;若把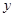 表示成
表示成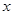 的函数,其解析式是
的函数,其解析式是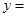 .
.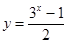
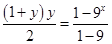 得:
得: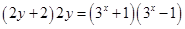
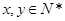 因此
因此 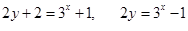
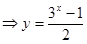 。
。