题目内容
设S,T是R的两个非空子集,如果存在一个从S到T的函数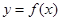 满足:
满足:
(i)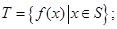 (ii)对任意
(ii)对任意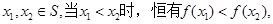
那么称这两个集合“保序同构”,现给出以下3对集合:
①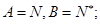
②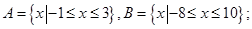
③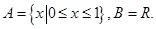
其中,“保序同构”的集合对的序号是_______.(写出“保序同构”的集合对的序号).
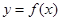 满足:
满足:(i)
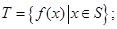 (ii)对任意
(ii)对任意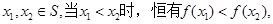
那么称这两个集合“保序同构”,现给出以下3对集合:
①
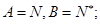
②
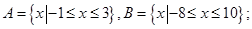
③
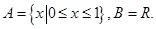
其中,“保序同构”的集合对的序号是_______.(写出“保序同构”的集合对的序号).
①②③
条件(i)说明S到T是一个一一映射,条件(ii)说明函数单调增.对于1可拟合函数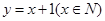 满足上述两个条件,故是保序同构;对于2可拟合函数
满足上述两个条件,故是保序同构;对于2可拟合函数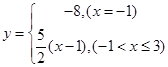 满足上述两个条件,故是保序同构;对于3可考虑经过平移压缩的正切函数也满足上述两个条件,故都是保序同构.
满足上述两个条件,故是保序同构;对于3可考虑经过平移压缩的正切函数也满足上述两个条件,故都是保序同构.
【考点定位】本题考查学生对新概念的理解,转化和应用,属于难题.
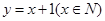 满足上述两个条件,故是保序同构;对于2可拟合函数
满足上述两个条件,故是保序同构;对于2可拟合函数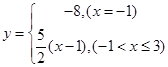 满足上述两个条件,故是保序同构;对于3可考虑经过平移压缩的正切函数也满足上述两个条件,故都是保序同构.
满足上述两个条件,故是保序同构;对于3可考虑经过平移压缩的正切函数也满足上述两个条件,故都是保序同构.【考点定位】本题考查学生对新概念的理解,转化和应用,属于难题.

练习册系列答案
相关题目
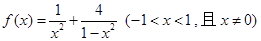 .
.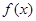 的最小值;
的最小值;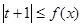 恒成立,求实数
恒成立,求实数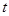 的取值范围.
的取值范围.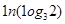
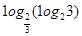
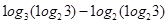
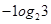
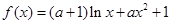 .
.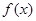 的单调性;
的单调性; 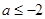 ,证明:对任意
,证明:对任意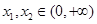 ,
,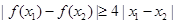 .
. .
.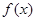 的单调性;
的单调性;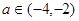 及
及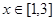 时,恒有
时,恒有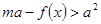 成立,求实数
成立,求实数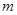 的取值范围.
的取值范围.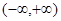 上的单调性,并用定义证明.
上的单调性,并用定义证明.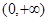 的函数
的函数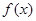 ,对任意的
,对任意的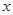 、
、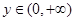 ,都有
,都有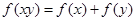 ,且当
,且当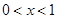 时,
时,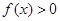 .
.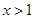 时,
时,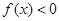 ;
;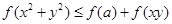 恒成立,求实数
恒成立,求实数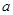 的取值范围.
的取值范围. ,则
,则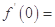 .
.