题目内容
(本小题满分14分)
已知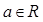 ,函数
,函数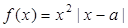 .
.
(Ⅰ)当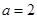 时,求使
时,求使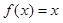 成立的
成立的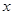 的集合;
的集合;
(Ⅱ)求函数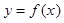 在区间
在区间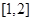 上的最小值.
上的最小值.
已知
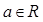 ,函数
,函数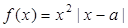 .
.(Ⅰ)当
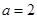 时,求使
时,求使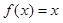 成立的
成立的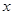 的集合;
的集合;(Ⅱ)求函数
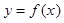 在区间
在区间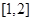 上的最小值.
上的最小值. (Ⅰ) 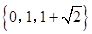 (Ⅱ)最小值为
(Ⅱ)最小值为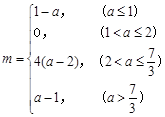
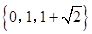 (Ⅱ)最小值为
(Ⅱ)最小值为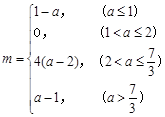
试题分析:(Ⅰ)由题意,
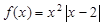 .
.当
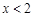 时,
时,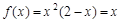 ,解得
,解得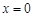 或
或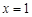 ;
;当
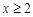 时,
时,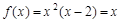 ,解得
,解得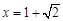 .
.综上,所求解集为
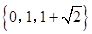 .
.(Ⅱ)设此最小值为
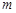 .
.①当
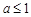 时,在区间
时,在区间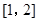 上,
上,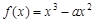 .
.因为
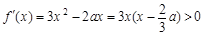 ,
,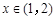 ,
,则
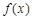 在区间
在区间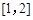 上是增函数,所以
上是增函数,所以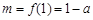 .
.②当
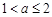 时,在区间
时,在区间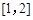 上,
上,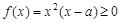 ,由
,由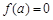 知
知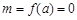 .
.③当
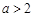 时,在区间
时,在区间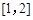 上,
上,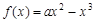 .
.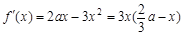 .
.若
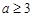 ,在区间
,在区间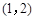 内
内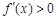 ,从而
,从而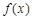 为区间
为区间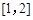 上的增函数,
上的增函数,由此得
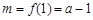 .
.若
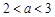 ,则
,则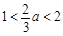 .
.当
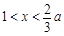 时,
时,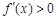 ,从而
,从而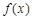 为区间
为区间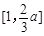 上的增函数;
上的增函数;当
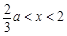 时,
时,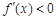 ,从而
,从而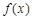 为区间
为区间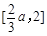 上的减函数.
上的减函数.因此,当
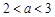 时,
时,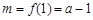 或
或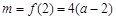 .
.当
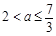 时,
时,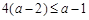 ,故
,故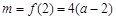 ;
;当
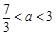 时,
时,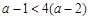 ,故
,故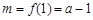 .
.综上所述,所求函数的最小值
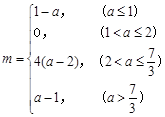
点评:求解含绝对值的不等式或函数问题,关键是通过讨论去掉绝对值符号,讨论的时候要注意做到“不重不漏”.

练习册系列答案
相关题目
 的函数
的函数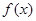 ,对任意的
,对任意的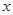 、
、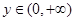 ,都有
,都有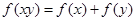 ,且当
,且当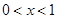 时,
时,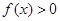 .
.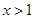 时,
时,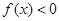 ;
;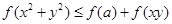 恒成立,求实数
恒成立,求实数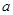 的取值范围.
的取值范围.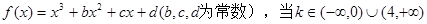 时,
时,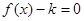 只有一个实根;当
只有一个实根;当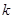 ∈(0,4)时,
∈(0,4)时,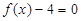 和
和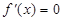 有一个相同的实根;
有一个相同的实根;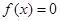 和
和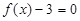 的任一实根大于
的任一实根大于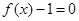 的任一实根;
的任一实根; 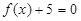 的任一实根小于
的任一实根小于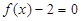 的任一实根.
的任一实根.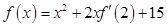 ,在闭区间
,在闭区间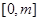 上有最大值15,最小值-1,则
上有最大值15,最小值-1,则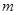 的取值范围是( )
的取值范围是( )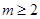
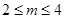
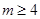

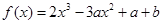 (其中a,b为实常数)。
(其中a,b为实常数)。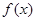 的单调区间:
的单调区间: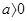 时,函数
时,函数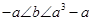 :
: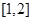 上是减函数,设关于x的方程
上是减函数,设关于x的方程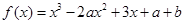 的两个非零实数根为
的两个非零实数根为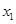 ,
,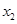 。试问是否存在实数m,使得
。试问是否存在实数m,使得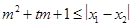 对任意满足条件的a及t
对任意满足条件的a及t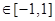 恒成立?若存在,求m的取值范围;若不存在,请说明理由。
恒成立?若存在,求m的取值范围;若不存在,请说明理由。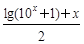 ,h (x)=
,h (x)=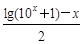
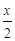 ,h (x)=lg(10x+1)-
,h (x)=lg(10x+1)-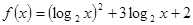 ,
,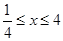 ,
,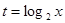 ,求
,求 取值范围;
取值范围; 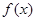 的最值,并给出函数取最值时对应的x的值。
的最值,并给出函数取最值时对应的x的值。 上的函数
上的函数 满足
满足 .当
.当 时,
时, ,当
,当 时,
时, 。则
。则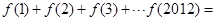 ( )
( )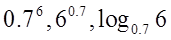 的大小顺序是__________。
的大小顺序是__________。