Question

【题目】已知椭圆 的离心率为 ，且过点
（Ⅰ）求椭圆 的方程；
（Ⅱ）设直线 与圆 相切于点 ，且 与椭圆 只有一个公共点 .
①求证： ；
②当 为何值时， 取得最大值？并求出最大值.

Answer 1

【答案】解：(I)椭圆E的方程为
（Ⅱ）①因为直线 与圆C: 相切于A,得 ,
即 ①
又因为 与椭圆E只有一个公共点B ，
由 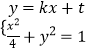得 ,且此方程有唯一解.
则 即
②由①②,得
②设 ，由 得
由韦达定理,
∵ 点在椭圆上,∴
∴
在直角三角形OAB中,

∴
【解析】（1）根据椭圆的性质得到，，再将点（，2）代入椭圆方程，解方程组即可得到。
（2）①根据直线与圆的位置关系，利用点到直线的距离公式可以得到t，k，R的等量关系；再根据直线与椭圆的交点为一个，联立方程，可得=0；结合两个等式，消去t2即可得到。
②因为是直角三角形，故根据勾股定理可得,而OA长为R，故要将B点坐标用R表示出来，代入等式即可得到AB的长度。