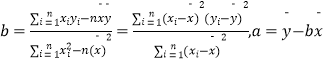题目内容
【题目】已知函数
(1)求f(x)的最小正周期及单调减区间；
(2)若α∈(0，π)，且f
＝
，求tan
的值．
【答案】（1）最小正周期
，单调减区间为
（2）
【解析】分析：（1）根据原式结合二倍角公式，降幂公式，辅助角公式进行化简，然后计算周期，根据正弦函数的基本性质求得单调区间；（2）∵f（
）＝
，即sin
＝1. 可得α的值，然后按正切的和差公式打开即可求解.
解：(1)f(x)＝(2cos2x－1)sin 2x＋
cos 4x
＝cos 2xsin 2x＋cos 4x
＝ (sin 4x＋cos 4x)
＝sin
，
∴f(x)的最小正周期T＝
.
令2kπ＋≤4x＋
≤2kπ＋
π，k∈Z，
得
＋
≤x≤＋
，k∈Z.
∴f(x)的单调减区间为
，k∈Z.
(2)∵f
＝，
即sin＝1.
因为α/span>∈(0，π)，－ <α－<
，
所以α－＝，故α＝.
因此tan
＝
＝
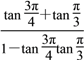＝2－
.
练习册系列答案
相关题目
