题目内容

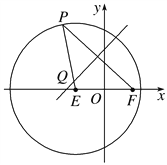
【题目】如图，已知圆，点是圆上任意一点，线段的垂直平分线和半径相交于.

(1)求动点的轨迹的方程；

(2)已知是轨迹的三个动点，点在一象限， 与关于原点对称，且，问的面积是否存在最小值？若存在，求出此最小值及相应直线的方程；若不存在，请说明理由.

【答案】（1）；（2）.

【解析】试题分析：（1）连接，根据题意， ，则 ，可得动点的轨迹是以为焦点，长轴长为的椭圆，即可求出动点的轨迹的方程；（2）设直线的方程为，与椭圆方程联立，求出的坐标，同理可得点的坐标，进而表示出的面积，利用基本不等式，即可得出结论.

试题解析：(1)∵Q在线段PF的垂直平分线上，∴|QP|＝|QF|，得|QE|＋|QF|＝|QE|＋|QP|＝|PE|＝4，

又|EF|＝2＜4，∴Q的轨迹是以E，F为焦点，长轴长为4的椭圆，∴Г： ＋y2＝1.

(2)由点A在第一象限，B与A关于原点对称，设直线AB的方程为y＝kx(k＞0)，

∵|CA|＝|CB|，∴C在AB的垂直平分线上，∴直线OC的方程为y＝－x. 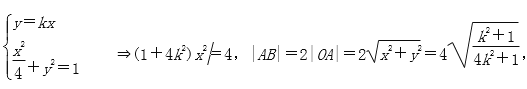，同理可得|OC|＝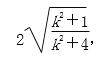

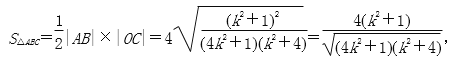
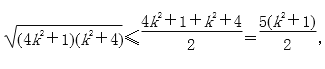当且仅当k＝1时取等号，∴S△ABC≥.

综上，当直线AB的方程为y＝x时，△ABC的面积有最小值.

练习册系列答案
相关题目

【题目】已知点，圆。

（1）若点在圆内，求的取值范围；

（2）若过点的圆的切线只有一条，求切线的方程；

（3）当时，过点的直线被圆截得的弦长为，求直线的方程。

【题目】[选修4-4：坐标系与参数方程]

在平面直角坐标系中，直线的参数方程为（为参数），在以直角坐标系的原点为极点， 轴的正半轴为极轴的极坐标系中，曲线的极坐标方程为.

（Ⅰ）求曲线的直角坐标方程和直线的普通方程；

（Ⅱ）若直线与曲线相交于， 两点，求的面积.

【题目】从某市主办的科技知识竞赛的学生成绩中随机选取了40名学生的成绩作为样本，已知这些成绩全部在40分至100分之间，现将成绩按如下方式分成6组：第一组；第二组；；第六组，并据此绘制了如图所示的频率分布直方图．

求成绩在区间内的学生人数；

估计这40名学生成绩的众数和中位数．

【题目】如图，河的两岸分别有生活小区和，其中，三点共线，与的延长线交于点，测得，，，，，若以所在直线分别为轴建立平面直角坐标系则河岸可看成是曲线（其中是常数）的一部分，河岸可看成是直线（其中为常数）的一部分．

（1）求的值．

（2）现准备建一座桥，其中分别在上，且，的横坐标为．写出桥的长关于的函数关系式，并标明定义域；当为何值时，取到最小值？最小值是多少？

【题目】设，曲线在点处的切线与直线垂直．

（1）求的值；

（2）若对于任意的恒成立，求的取值范围．

【题目】已知集合M＝{x|x<－3，或x>5}，P＝{x|(x－a)·(x－8)≤0}．

(1)求M∩P＝{x|5<x≤8}的充要条件；

(2)求实数a的一个值，使它成为M∩P＝{x|5<x≤8}的一个充分但不必要条件．

【题目】已知椭圆的离心率为，且过点．

（Ⅰ）求椭圆的方程．

（Ⅱ）若， 是椭圆上两个不同的动点，且使的角平分线垂直于轴，试判断直线的斜率是否为定值？若是，求出该值；若不是，说明理由．

【题目】已知椭圆（）的上顶点与抛物线（）的焦点重合.

（1）设椭圆和抛物线交于， 两点，若，求椭圆的方程；

（2）设直线与抛物线和椭圆均相切，切点分别为， ，记的面积为，求证： .

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网